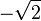Sous-corps exotique de R - Définition
Nous construisons ici un exemple de sous-corps indénombrable strict de

Soit E l'ensemble des sous-corps de



![K[\sqrt{2}] \to \mathbb{R}](https://static.techno-science.net/illustration/Definitions/autres/d/d2c499835317acad6842807510cf6dfc_3b886082d43edbe5b6710eee720ba11c.png)
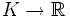


![K[\sqrt{2}]](https://static.techno-science.net/illustration/Definitions/autres/4/4e5a317b30a3d5162080504cf08dae4c_c6f7cf84d3e120a5b8bf39c60aea434d.png)

![K[\sqrt{2}]](https://static.techno-science.net/illustration/Definitions/autres/4/4e5a317b30a3d5162080504cf08dae4c_c6f7cf84d3e120a5b8bf39c60aea434d.png)

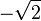

Nous construisons ici un exemple de sous-corps indénombrable strict de

Soit E l'ensemble des sous-corps de



![K[\sqrt{2}] \to \mathbb{R}](https://static.techno-science.net/illustration/Definitions/autres/d/d2c499835317acad6842807510cf6dfc_3b886082d43edbe5b6710eee720ba11c.png)
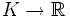


![K[\sqrt{2}]](https://static.techno-science.net/illustration/Definitions/autres/4/4e5a317b30a3d5162080504cf08dae4c_c6f7cf84d3e120a5b8bf39c60aea434d.png)

![K[\sqrt{2}]](https://static.techno-science.net/illustration/Definitions/autres/4/4e5a317b30a3d5162080504cf08dae4c_c6f7cf84d3e120a5b8bf39c60aea434d.png)