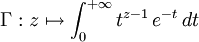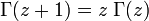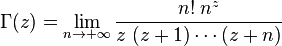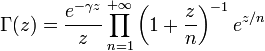Fonction gamma - Définition
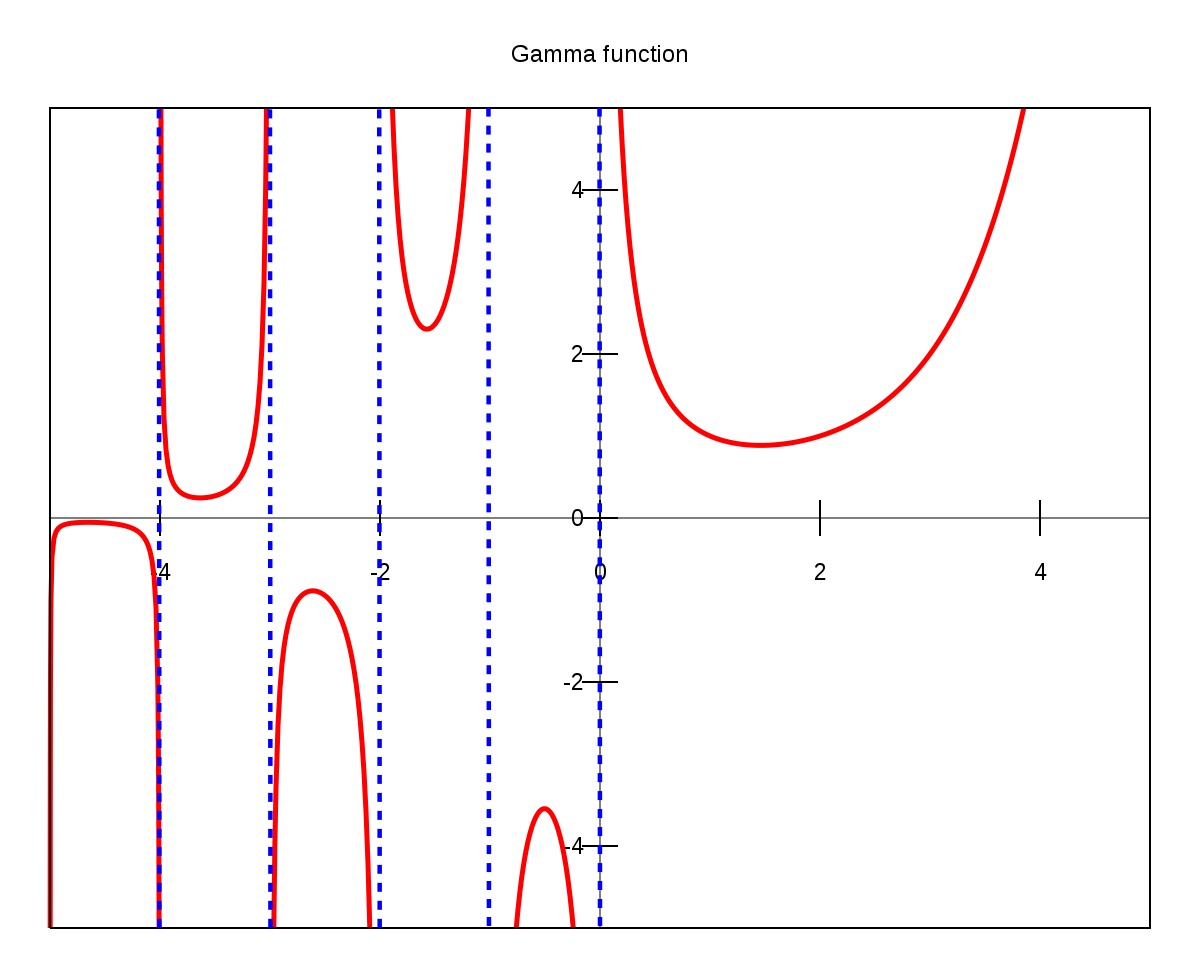
La fonction gamma est, en mathématiques, une fonction complexe.
Elle prolonge la fonction factorielle à l'ensemble des nombres complexes (excepté en certains points).
Définition
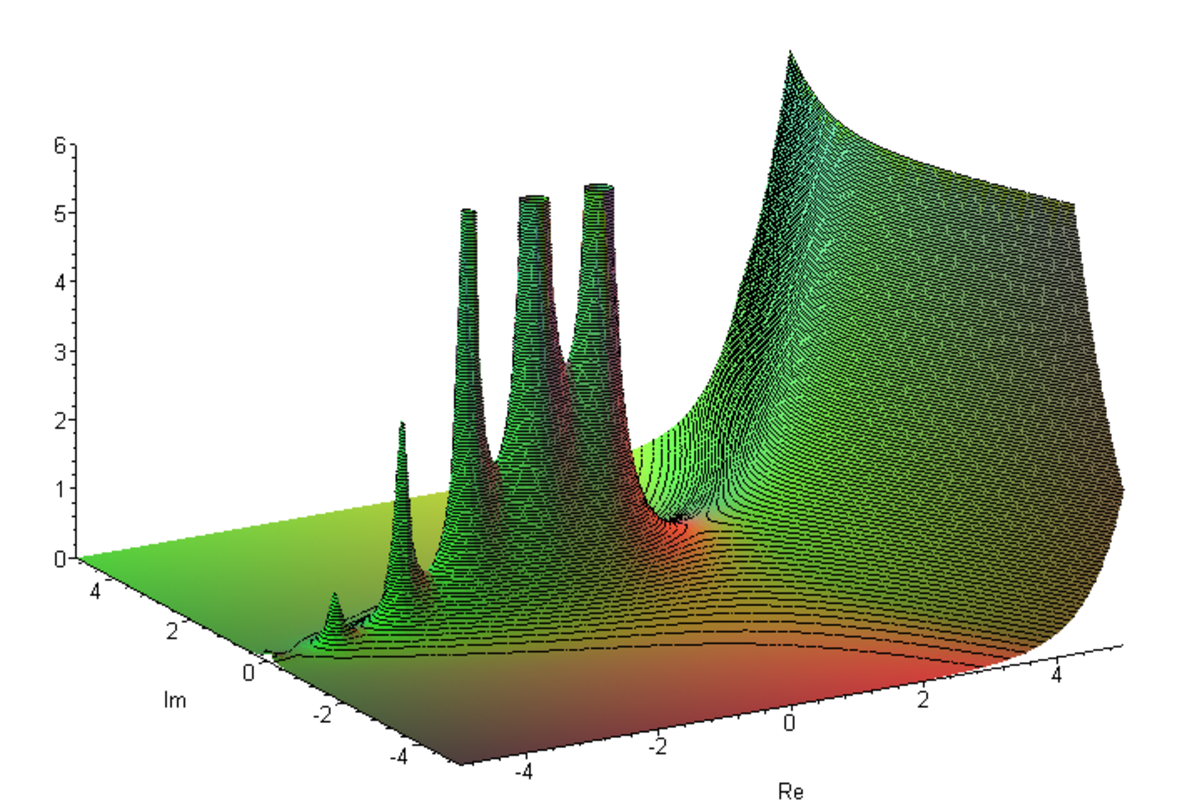
Pour 
tel que 
0\," />, on définit la fonction suivante :
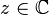
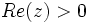
Cette intégrale converge absolument sur le demi-plan complexe où la partie réelle est strictement positive.
En intégrant par parties, on montre que :
Cette fonction peut être ainsi prolongée analytiquement en une fonction méromorphe sur l'ensemble des nombres complexes, excepté pour z = 0, −1, −2, −3, ... qui sont des pôles. C'est ce prolongement qu'on appelle généralement "fonction gamma".
Autres définitions
Les définitions suivantes de la fonction gamma par produits infinis, dues respectivement à Euler et Weierstrass, ont un sens pour les nombres complexes z qui ne sont pas des entiers négatifs ou nuls :
où γ est la constante d'Euler-Mascheroni.