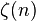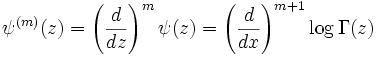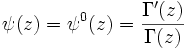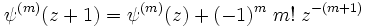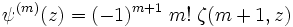Fonction polygamma - Définition

En mathématiques, la fonction polygamma d'ordre m est définie comme la m+1 -ième dérivée logarithmique de la fonction gamma :

Ici,

est la fonction digamma et est la fonction gamma.

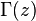
Elle possède la relation de récurrence

Elle est reliée à la fonction Zeta d'Hurwitz

La série de Taylor au point z=1 est

,

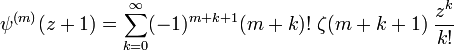
qui converge pour |z|<1. Ici, est la fonction Zeta de Riemann.