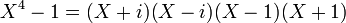On considère ici des polynômes de degré supérieur ou égal à 1, à coefficients dans un corps commutatif . On appelle factorisation d'un polynôme P l'écriture de ce polynôme sous forme d'un produit de polynômes dont les degrés sont strictement inférieurs à celui de P.

Un polynôme (En mathématiques, un polynôme est la combinaison linéaire des puissances d'une variable, habituellement notée X. Ces objets sont largement utilisés en pratique, ne...) n'admettant pas de factorisation (au sens (SENS (Strategies for Engineered Negligible Senescence) est un projet scientifique qui a pour but l'extension radicale de l'espérance de vie humaine. Par une évolution...) précédent) est dit irréductible ; c'est notamment le cas des polynômes de degré (Le mot degré a plusieurs significations, il est notamment employé dans les domaines suivants :) 1. Un théorème (Un théorème est une proposition qui peut être mathématiquement démontrée, c'est-à-dire une assertion qui peut être établie comme vraie au travers d'un raisonnement logique...) classique est l'existence, sur un anneau factoriel, pour tout (Le tout compris comme ensemble de ce qui existe est souvent interprété comme le monde ou l'univers.) polynôme non irréductible, d'une factorisation en produit de polynômes irréductibles ; cette factorisation est essentiellement unique, à permutation (En mathématiques, la notion de permutation exprime l'idée de réarrangement d'objets discernables. Une permutation de n objets distincts rangés dans un certain ordre, correspond à un changement...) près des facteurs et aux inversibles près.

Des algorithmes de factorisation des polynômes (On considère ici des polynômes de degré supérieur ou égal à 1, à coefficients dans un corps commutatif . On appelle factorisation d'un polynôme P l'écriture de ce polynôme sous forme...) à coefficients dans les corps finis sont connus, par exemple l'algorithme de Berlekamp.

Cas usuels

Deux cas fréquents sont ceux des polynômes à coefficients dans et des polynômes à coefficients dans .

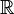
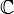
• Les seuls polynômes irréductibles de sont les polynômes de degré 1 : tout polynôme de degré n à coefficients complexes peut se factoriser dans en produit de n polynômes du premier degré. C'est le théorème fondamental de l’algèbre, ou théorème de d'Alembert-Gauss.

• Les polynômes irréductibles de sont de deux sortes : les polynômes de degré 1, et les polynômes de degré 2 sans racines réelles : tout polynôme P à coefficients réels peut se factoriser dans en produit de polynômes de degré 1 (dont les racines sont les racines réelles de P) et / ou de polynômes de degré 2 sans racines réelles (dont les racines, deux à deux conjuguées dans , sont les racines non réelles de P).

Exemples

Considérons le polynôme à coefficients dans ou .

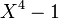
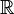
• L'identité remarquable donne :

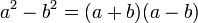
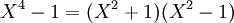
puis :

.

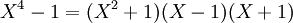
Ceci est la factorisation en produit de facteurs irréductibles à coefficients dans .

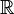
• La factorisation en produit de facteurs irréductibles à coefficients dans est :

.