Anneau factoriel - Définition

Introduction

En mathématiques, un anneau factoriel est un cas particulier d'anneau commutatif, unitaire et intègre. À l'image des nombres entiers, il existe un équivalent du théorème fondamental de l'arithmétique pour une telle structure. Tout élément d'un anneau factoriel se décompose en un produit d'un élément inversible et d'éléments irréductibles. Un élément irréductible est un élément qui, dans une décomposition en produit de deux facteurs, contient toujours un élément inversible. Par exemple dans Z, l'anneau des entiers relatifs, -2 est irréductible. La décomposition en facteurs irréductibles est unique dans un anneau factoriel, aux éléments inversibles près.

Les exemples d' anneau factoriel ne sont pas rares. Tout anneau principal (c'est-à-dire dont tout idéal est principal) est factoriel. La réciproque n'est pas vraie. Ainsi un anneau de polynômes à coefficients dans un anneau factoriel k est toujours factoriel lui aussi, mais n'est principal que si l'anneau k est un corps. En ce sens, le concept d'anneau factoriel généralise celui d'anneau principal.

Certains résultats usuels de l'arithmétique élémentaire s'appliquent sur un anneau factoriel. Ainsi, le lemme d'Euclide est vérifié et il est possible de définir un plus grand commun diviseur et un plus petit commun multiple bénéficiant presque des propriétés usuelles sur Z.

Définitions

Dans tout ce paragraphe, A désigne un anneau commutatif, unitaire et intègre. Le groupe des unités est constitué des éléments qui possèdent un inverse dans A.

La notion d'anneau factoriel s'appuie sur les deux définitions :

• Un élément non nul a de A est dit irréductible s'il n'est pas inversible et si toute décomposition en deux facteurs b et c de a, a = b.c comporte un élément inversible (soit b soit c).

• Deux éléments a et b non nuls de A sont dit associés s'il existe un élément inversible u tel que a = u.b. Cette relation est une relation d'équivalence.

La définition la plus courante d'anneau factoriel est :

• A est dit factoriel s'il vérifie les deux propriétés suivantes :

(1) Pour tout élément a de A, non nul et non inversible, il existe une suite finie p₁, …, p_n d'éléments irréductibles de A tels que :

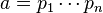
(2) La décomposition est unique à permutation près des p_i et à produit près de ceux-ci par des éléments inversibles.

Exemple : L'anneau Z des entiers relatifs est factoriel. Ses éléments inversibles sont -1 et 1, donc deux entiers non nuls sont associés lorsqu'ils sont égaux ou opposés. Ses éléments irréductibles sont les entiers naturels premiers et leurs opposés. Tout élément non nul de Z se décompose en un produit d'éléments irréductibles. Par exemple, -28 se décompose en (-2).2.7. On pourrait aussi le décomposer par exemple en (-7).2.2 mais cette dernière décomposition est considérée comme la même que la première, car elle s'en déduit en permutant les facteurs et en les multipliant par des inversibles.

Certains anneaux possèdent des éléments irréductibles particuliers, ainsi un élément irréductible et positif de Z est appelé nombre premier. Dans K[X] (si K est un corps), les éléments particuliers sont les polynômes irréductibles unitaires, c'est-à-dire dont le coefficient du monôme dominant est égal à un. Chaque classe d'équivalence contient un unique élément irréductible particulier. Cette approche permet de normaliser la décomposition en facteurs irréductibles de telle sorte que l'unicité soit absolue, et plus seulement à permutation et association près.

Il est toujours possible d'établir une normalisation de cette nature. Il suffit de définir une famille (p_i) d'éléments irréductibles tel que si i est différent de j alors p_i n'est pas associé à p_j et si π est un élément irréductible il existe un indice i tel que π est associé à p_i. L'axiome du choix montre qu'il est toujours possible de trouver une famille maximale d'éléments irréductibles deux à deux non associés : on prend un représentant par classe d'association d'éléments irréductibles. Cette normalisation est utilisée dans la suite de l'article : elle n'est pas nécessaire mais permet d'alléger les énoncés. Un élément a non nul d'un anneau factoriel s'écrit ainsi de façon unique :

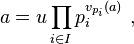
où u est un élément inversible. La fonction v_pi, de A dans l'ensemble N des entiers naturels, s'appelle une valuation p-adique. La valeur v_pi(a) est aussi appelée ordre de multiplicité de p_i dans a.

Dans la suite de l'article A désigne un anneau factoriel et (p_i) une telle famille d'éléments irréductibles (sauf mention explicite contraire).