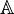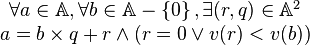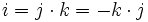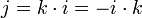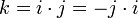Quaternions d'Hurwitz - Définition
Definition
Quaternions
Soit 
un anneau. On definit l'algèbre des quaternions 
comme le -module libre engendré par 1, i, j et k, muni de la structure d'algèbre :
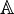
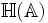
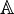
- 1 élement neutre pour la multiplication
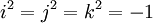
- et les identités:
Quaternions d'Hurwitz
Soit 
, l'algèbre des quaternions sur l'anneau 
. On définit les Quaternions d'Hurwitz 
comme suit:
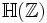
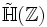
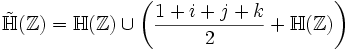
On peut aussi definir les Quaternions d'Hurwitz comme:
les Quaternions d'Hurwitz sont un sous-anneau de 
, dont les éléments: 
sont tels que 2a, 2b, 2c et 2d sont entiers (
).
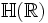
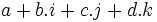
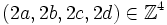
Propriétés
Les Quaternions d'Hurwitz forment un anneau euclidien à gauche et à droite.
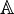
Un anneau est dit euclidien si
est intègre- est muni d'une division euclidienne i.e. il existe une application v telle que:
Populaires