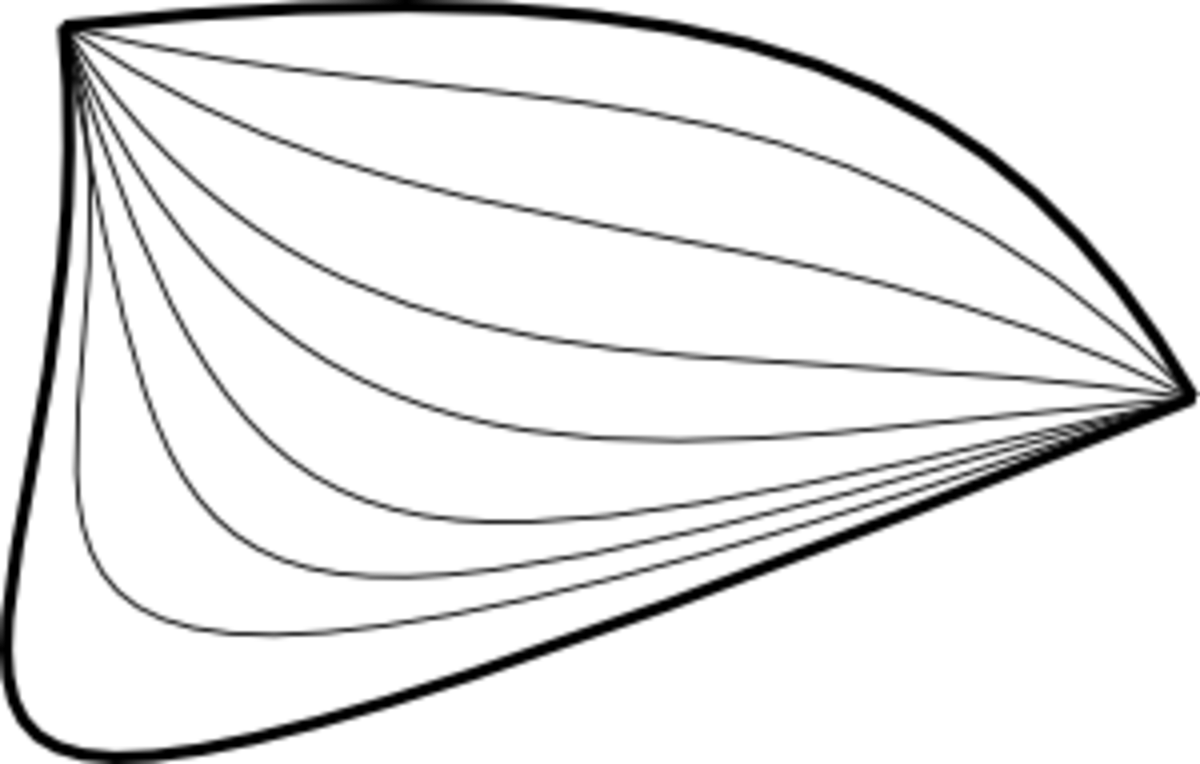
Homotopie - Définition
En mathématiques, le concept topologique d'homotopie formalise la notion naturelle de " déformation continue " d'un objet vers un autre.
Homotopie entre fonctions
On se donne deux espaces topologiques

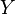
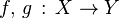
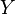
![H \, : \, X \times [0,1] \rightarrow Y \,\!](https://static.techno-science.net/illustration/Definitions/autres/6/678f38ea0cd6420b94118ea72e528cf0_cb3b3eaa5b165f6e3609db7ad7a22e20.png)
Autrement dit, selon les valeurs du paramètre
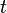
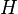
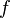
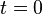
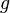
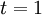
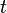
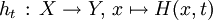
" située entre
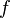
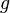
Une autre manière de le voir est que pour chaque
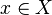
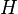
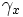
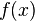
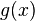
![\gamma_x \, : \, [0,1] \rightarrow Y, \, t \mapsto H(x,t) \,\!](https://static.techno-science.net/illustration/Definitions/autres/e/e4b18e2fbb25bc9fb2319fe5a53b95cd_cc2aeb17d1a3d759672dd579df481012.png)
Exemple 1 : On prend
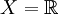
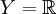
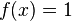
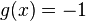
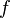
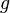
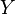
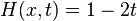
(à noter que dans cet exemple rien ne dépend de la variable
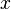
- NB : La mention " homotope dans
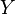
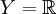
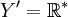
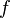
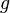
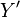
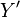
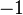
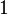
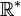
Exemple 2 : On prend
![X = [0,1] \,\!](https://static.techno-science.net/illustration/Definitions/autres/f/fc858ecf7dce75a89828944e7068fae2_f96ce4fe3af3219cc8ddcf4e52a5f921.png)
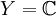
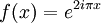
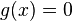
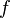
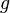
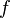
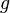
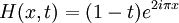
(pour chaque valeur de
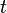
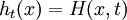
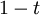
L'homotopie des fonctions est une relation d'équivalence sur l'ensemble
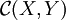

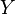
Équivalence homotopique entre espaces topologiques
La définition de l'homotopie entre deux espaces peut paraître abstraite, mais elle correspond à l'idée très simple de déformation continue.
Étant donné deux espaces topologiques
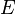
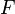
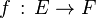
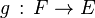
-
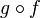
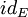
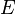
-
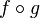
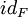
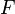
On parlera plus souvent d'équivalence homotopique entre deux parties d'espaces topologiques.
Deux espaces topologiques homéomorphes sont homotopiquement équivalents mais la réciproque est fausse en général, comme le montrent les exemples suivants.
Exemples :
- Un cercle, une ellipse sont homotopiquement équivalents à
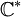
- Un segment
![[a,b] \,\!](https://static.techno-science.net/illustration/Definitions/autres/8/8b596d04e319e05cadcc7dcf251a9815_d0fd2a02aef5c5cb89aaff8e4ffed7c8.png)
L'équivalence homotopique est une relation d'équivalence entre espaces topologiques. Diverses propriétés importantes en Topologie algébrique sont conservées par équivalence homotopique, parmi lesquelles : la connexité simple, la connexité par arcs, les groupes d'homologie et de cohomologie...
Isotopie
L' isotopie est un raffinement de l'homotopie ; dans le cas où les deux applications continues
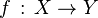
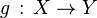
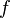
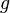
On dira donc que
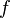
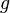
![H \, : \, X \times [0,1] \rightarrow Y \,\!](https://static.techno-science.net/illustration/Definitions/autres/6/678f38ea0cd6420b94118ea72e528cf0_cb3b3eaa5b165f6e3609db7ad7a22e20.png)
-
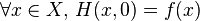
-
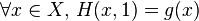
- pour tout
![t \in [0,1] \,\!](https://static.techno-science.net/illustration/Definitions/autres/b/bfa0f1f24a438981cb0253c333596893_6f8fbc3415fcc374acc2df495ca8d332.png)
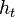
La fonction
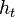
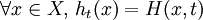
La notion d'isotopie est notamment importante en théorie des nœuds : deux nœuds sont considérés identiques s'ils sont homotopes, c'est-à-dire si on peut déformer l'un pour obtenir l'autre sans que la " corde " se déchire ou se pénètre.