Fonction harmonique - Définition
En mathématiques, une fonction harmonique est une fonction deux fois continûment dérivable :
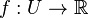

-
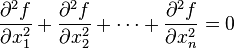
On écrit aussi :
-
-
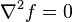
-
Un exemple particulier est constitué des fonctions partie réelle et partie imaginaire déduites d'une fonction holomorphe.
Un problème classique concernant les fonctions harmoniques est le problème de Dirichlet : une fonction continue étant donnée sur la frontière d'un ouvert, peut-on la prolonger en une fonction harmonique dans tout l'intérieur de cet ouvert?

















































