Événement (mathématiques) - Définition

En théorie des probabilités, un événement est un ensemble de résultats d'une épreuve aléatoire (un sous-ensemble de l'univers). Un événement étant souvent défini par une proposition, nous devons pouvoir dire, pour tout résultat de l'univers, si l'événement se réalise ou non.

Mathématiquement, un événement est un élément d'une σ-algèbre d'un espace probabilisable .

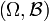
Opérations ensemblistes sur les événements

• Soit l'événement X suivant composé de deux événements simples :

(lire " A union B ")

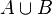
La réalisation de cet événement entraîne la réalisation de l'événement A ou de l'événement B, ou des deux événements A et B simultanément.

• Soit l'événement Y suivant composé de deux événements simples :

(lire " A inter B ")

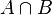
La réalisation de cet événement entraîne la réalisation de l'événement A et de l'événement B.

• La relation suivante signifie que la réalisation de l'événement A implique automatiquement celle de l'événement B.

(lire " A inclus dans B ")

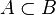
Expressions ensemblistes d'événements aléatoires

Soient A, B, C trois événements.

Crescendo, six cas probables s'offrent à l'expérience :

• Aucun événement ne se produit :

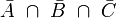
• Un seul événement se produit :

• Au moins un événement se produit :

• Deux événements au plus se produisent :

• Au moins deux événements se produisent :

• Les trois événements se produisent :

(Les formules peuvent êtres généralisées à un ensemble N d'événements.)

Exemples

• L'univers Ω est un événement, appelé événement certain.
• L'ensemble vide est un événement, appelé événement impossible.
• pour tout ω appartenant à Ω le singleton {ω} est un événement, appelé événement élémentaire.
• Nous disposons 52 cartes et deux jokers sur une table et nous tirons une seule carte. Tirer une carte individuelle dans l'univers des 54 cartes, représente un événement élémentaire. Mais les sous-ensembles (y compris les événements élémentaires) sont simplement appelés des " événements ". Des événements de cet univers peuvent être :
  • " obtenir un roi " ensemble constitué des 4 rois (union de 4 évènements élémentaires),
  • " obtenir une carte de cœur " (ensemble de 13 cartes)
  • " obtenir une figure " (ensemble de 12 cartes).