Algorithme de Kruskal - Définition
L'algorithme de Kruskal est un algorithme de recherche d'arbre recouvrant de poids minimum (ARPM) ou arbre couvrant minimum (ACM).
Description du problème
Quand on travaille sur un graphe connexe, certains problèmes obligent à transformer ce graphe en un arbre (graphe sans cycle) qui contient tous les sommets du graphe et quelques arêtes. On dit alors qu'on a un arbre couvrant du graphe.
- Exemples :
- Simplifier un cablage
Parfois, lorsque le graphe est valué, il s'agit de chercher un arbre recouvrant de poids minimum, c'est-à-dire dont la somme des poids est minimale.
- Exemples :
- Supprimer les liaisons maritimes les moins rentables en preservant l'accessibilité aux differents ports.
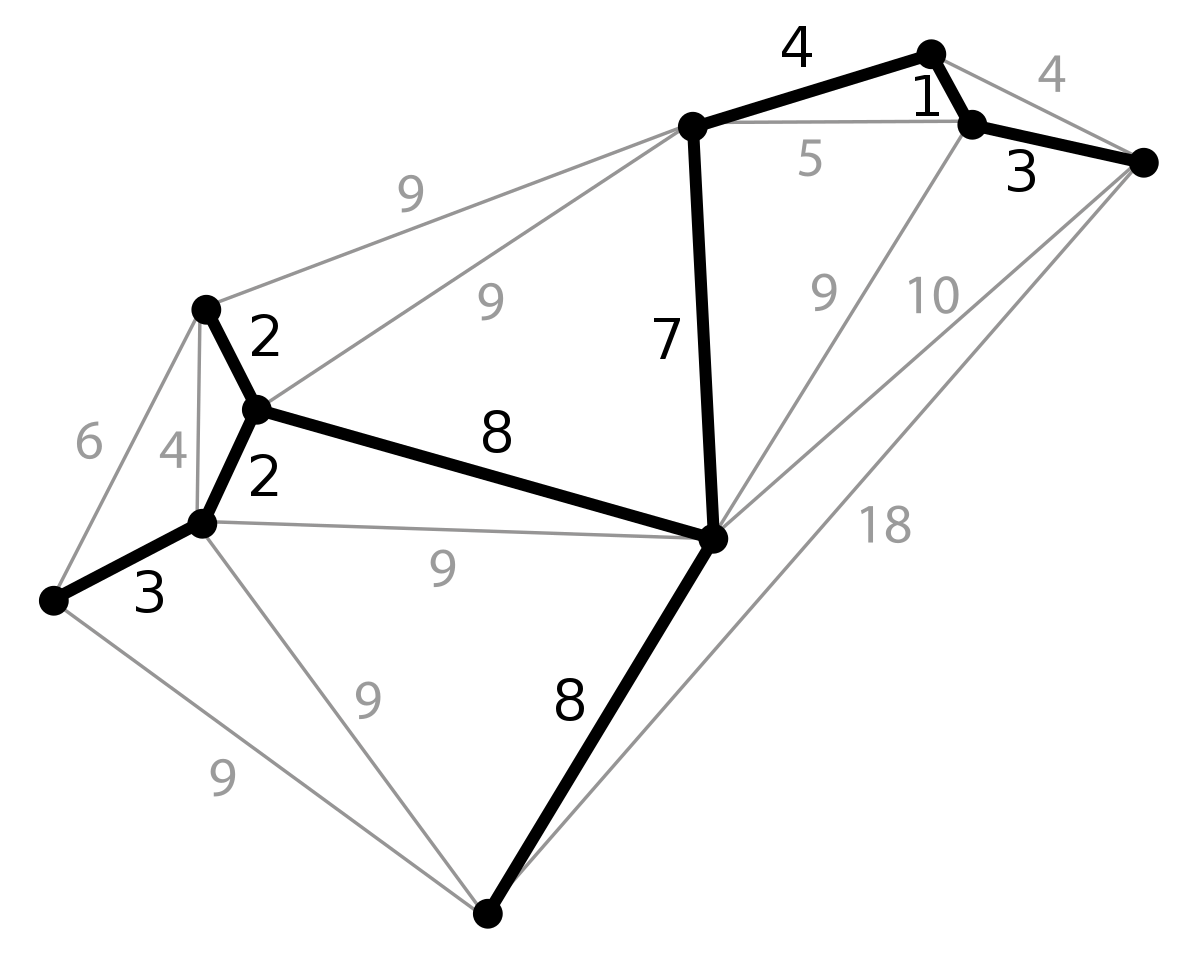
L'ARPM contient tous les sommets du graphe qu'il recouvre et uniquement les arêtes qui assurent son acyclicité et le poids minimum possible.
Principe
L'algorithme consiste à d'abord ranger par ordre de poids croissant les arêtes d'un graphe, puis à retirer une à une les arêtes selon cet ordre et à les ajouter à l'ACM cherché tant que cet ajout ne fait pas apparaître un cycle dans l'ACM.0
Algorithme
KRUSKAL (G,w)
1 E:= ø
2 pour chaque sommet v de G
3 faire CRÉER-ENSEMBLE (v)
4 trier les arêtes de G par ordre croissant de poids w
5 pour chaque arête (u,v) de G prise par ordre de poids croissant
6 faire si ENSEMBLE-REPRÉSENTATIF (u) ≠ ENSEMBLE-REPRÉSENTATIF (v)
7 alors ajouter l'arête (u,v) à l'ensemble E
8 UNION (u,v)
9 retourner E
w est une fonction qui associe à chaque arête du graphe G une valeur qui est son poids. La fonction ENSEMBLE-REPRÉSENTATIF(e) retourne un élément représentatif d'un ensemble. UNION(u,v) combine les arbres obtenus au fur et à mesure.
La complexité de l'algorithme est Θ(A log S) avec A le nombre d'arêtes et S le nombre de sommets du graphe G. On remarquera que lors du déroulement de l'algorithme, l'ACM n'est pas connexe, il ne le sera qu'à la fin.