Principe de correspondance - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En physique, le principe de correspondance, proposé pour la première fois par Niels Bohr en 1923, est un principe établissant que le comportement quantique d'un système peut se réduire à un comportement de physique classique, quand les nombres quantiques mis en jeu dans le système sont très grands, ou quand la quantité d'action représentée par la constante de Planck peut être négligée devant l'action mise en oeuvre dans le système.
Origine et nécessité
Les lois de la mécanique quantique sont extrêmement efficaces dans la description des objets microscopiques, comme les atomes ou les particules. D'un autre côté, l'expérience révèle que de nombreux systèmes macroscopiques - par exemple les ressorts ou les condensateurs - peuvent être tout à fait décrits par des théories classiques, ne faisant intervenir que la mécanique newtonienne et l'électromagnétisme non relativiste. Ainsi, puisqu'il n'y a pas de raison particulière pour que les lois de la physique, supposées universelles, dépendent de la taille d'un système, Bohr proposa ce principe, selon lequel : « La mécanique classique doit se retrouver, comme approximation de la mécanique quantique pour des objets plus gros ».
Cette formule est cependant ambiguë : quand doit-on considérer qu'un système n'est plus soumis aux lois classiques ? La physique quantique pose une limite de correspondance, ou limite classique. Bohr a fourni une mesure grossière de cette limite : « quand les nombres quantiques décrivant le système sont grands », ce qui signifie soit que le système est très énergétique, soit qu'il est constitué de beaucoup de nombres quantiques, soit les deux.
Le principe de correspondance est l'un des outils fondamentaux qui permettent de vérifier les théories quantiques qui ont une réalité. En effet, la formulation - très mathématique - de la physique quantique est très ouverte : on sait par exemple que les états d'un système physique occupent un espace de Hilbert, mais on ne sait rien de cet espace. Le principe de correspondance limite ainsi les choix, quand ils se présentent, à des solutions qui ne contredisent pas la mécanique classique à grande échelle.
Expression mathématique du principe de correspondance
On peut passer de lois en physique classique aux lois traitant du même sujet en physique quantique en :
- Remplaçant les variables dynamiques V du système par des observables A agissant sur la fonction d'état du système.
- Remplaçant
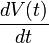
![\frac{1}{i\hbar} [H;A(t)]](https://static.techno-science.net/illustration/Definitions/autres/3/3135c8dab757776607777aa70b1d128d_842cbaca02c63f6ae5511a9b5c42ee91.png)
![\frac{1}{i\hbar} [H;A(t)]](https://static.techno-science.net/illustrationWebp/Definitions/autres/3/3135c8dab757776607777aa70b1d128d_842cbaca02c63f6ae5511a9b5c42ee91.png)
On peut démontrer que
![\frac{1}{i\hbar} [H;A(t)] = \left\{ H,A \right\} + O(\hbar^2)](https://static.techno-science.net/illustrationWebp/Definitions/autres/e/e9d0a5a3ef58749f51b223c02169c4ea_73a00f8c33a924ebfd1f480f68d16651.png)
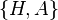
Or,
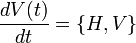
Ce qui aboutit au théorème d'Ehrenfest : les mesures faites en physique classique sont égales aux moyennes des observables associés aux variables utilisées.
(Cependant il faut remarquer, qu' en mécanique quantique il y a des propriétés sans correspondance classique, p. ex. spin.)
Exemples
Oscillateur harmonique quantique
Il est montré ici en quoi, dans cet exemple, des nombres quantiques importants permettent de retrouver la mécanique classique.
On considère un oscillateur harmonique quantique à 1 dimension. D'après la mécanique quantique, son énergie totale (cinétique et potentielle), notée E, est l'une des valeurs discrètes :
où
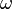
C'est ici qu'intervient le principe de correspondance, qui permet de passer à un cas « macroscopique ». En notant
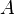
À la limite de correspondance, les deux approches sont équivalentes : la mécanique quantique donne :
Prenons des valeurs à notre échelle : m = 1 kg,
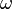
On comprend alors pourquoi on a l'impression d'un mouvement continu : avec
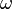
Équation de Schrödinger
L'équation de l'énergie d'un corps en physique classique est :
La correspondance entre les valeurs classiques et les opérateurs est :
En remplaçant dans l'énergie classique, on obtient :
Cette égalité est une égalité d'opérateurs agissants sur l'ensemble des fonctions. En l'appliquant à une fonction
Ce qui n'est rien d'autre que l'équation de Schrödinger.
Cette manière de l'obtenir n'a qu'une vertu d'illustration de l'utilisation du principe et n'est nullement une démonstration de l'équation.
Il est à remarquer que cette technique appliquée à l'équation de l'énergie en relativité restreinte permet de retrouver l'équation de Klein-Gordon.
