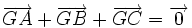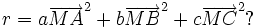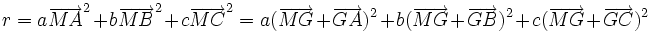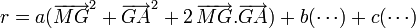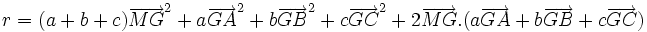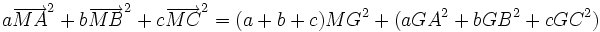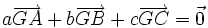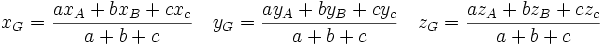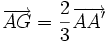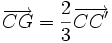Barycentre (géométrie élémentaire) - Définition

Barycentre de n points

On peut généraliser la définition à n points dans un espace affine E quelconque. On définit alors une fonction f de E dans , appelée fonction vectorielle de Leibniz :

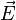
On démontre que si est non nul, la fonction s'annule pour un unique point G appelé barycentre du système {(A_i,a_i)}_{i = 1...n}. Ce point G est toujours dans le sous-espace affine engendré par les (A_i). Réciproquement, si les A_i constituent une famille libre de n points d'un sous-espace affine F de dimension n - 1, tout point M de F peut s'écrire comme barycentre des points (A_i). Les pondérations s'appellent les coordonnées barycentriques de G dans le repère (A_i).

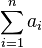
Réduction de fonctions vectorielles ou du second degré

À partir du barycentre, il est possible de réduire des expressions vectorielles. Prenons l'exemple de 3 points seulement A B C de poids a b c et leur barycentre G. La formule du premier degré est celle du barycentre :

qui permet de nombreux calculs du premier degré sur les vecteurs.

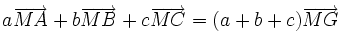
A partir du barycentre il est possible de définir une formule du second degré, au sens du produit scalaire des vecteurs : Que peut-on dire de la formule du second degré suivante, dont le résultat est un nombre r

Remplaçons chaque vecteur etc par et appliquons la formule du carré d'une somme:

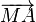
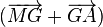
Les doubles produits s'annulent, d'où le résultat

au second degré où seul le terme MG² est variable.

Rappelons la formule de départ du premier degré

Exemple pratique

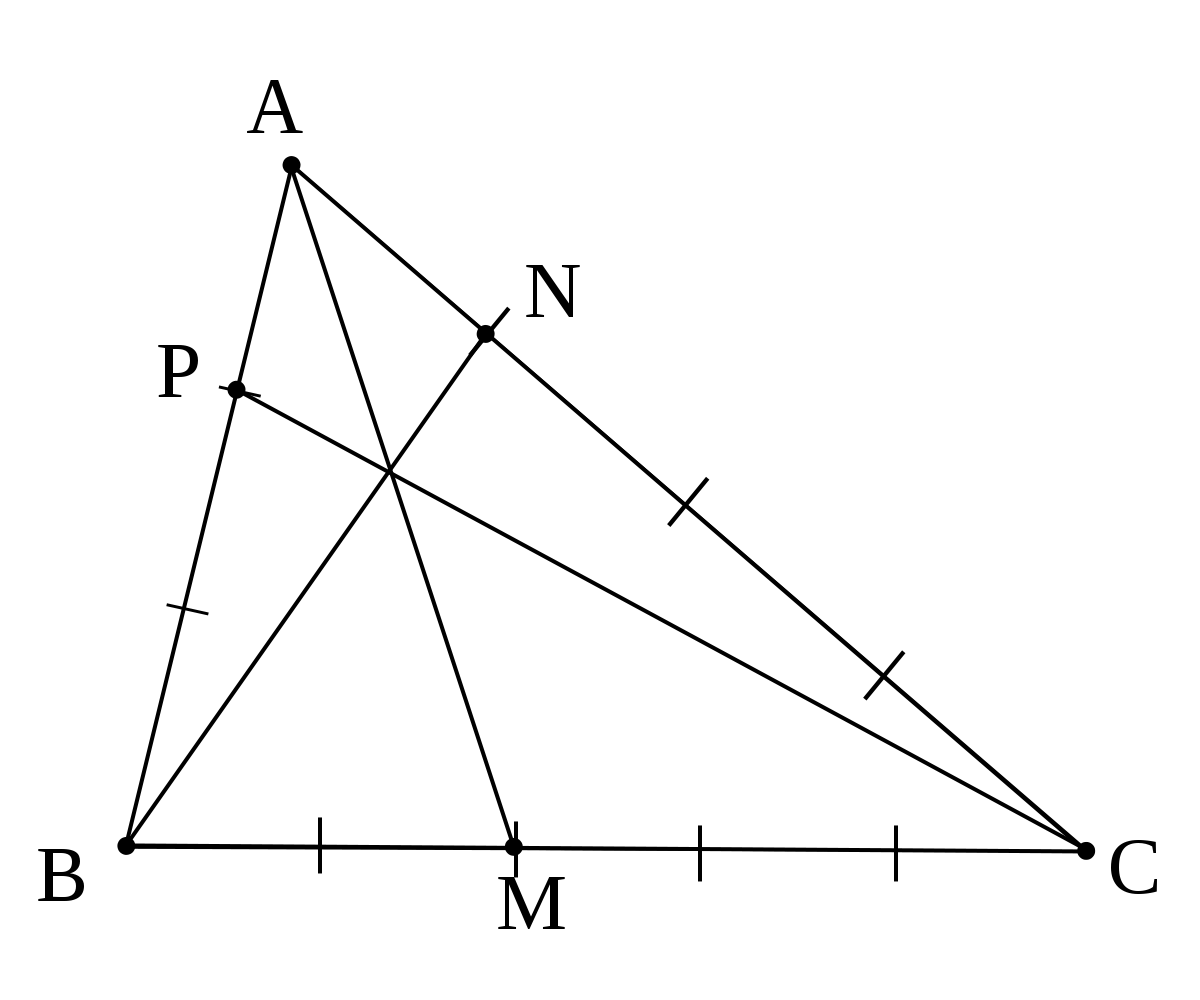
Dans le dessin ci-contre (figure 2), les graduations sur chaque côté sont régulières. Les droites (AM) (BN) et (CP) sont concourantes.

Démonstration

La lecture du dessin permet de dire que

• P est barycentre du système {(A ; 2), (B ; 1)}
• N est barycentre du système {(A ; 3), (C ; 1)}
• M est barycentre du système {(B ; 3), (C ; 2)}

La propriété d'homogénéité du barycentre permet de dire que

• P est barycentre du système {(A ; 6), (B ; 3)}
• N est barycentre du système {(A ; 6), (C ; 2)}
• M est barycentre du système {(B ; 3), (C ; 2)}

Il suffit alors de créer un point G barycentre du système {(A ; 6) , (B ; 3) ; (C ; 2)} et d'utiliser trois fois la propriété d'associativité

• G est barycentre du système {(P ; 9), (C ; 2)} donc G est sur la droite (PC)
• G est barycentre du système {(N ; 8), (B ; 3)} donc G est sur la droite (NB)
• G est barycentre du système {(M ; 5), (A ; 6)} donc G est sur la droite (AM)

G est donc le point de concours des trois droites.

Barycentre de trois points dans le plan ou dans l'espace

La définition peut se généraliser à trois points : pour tous réels a, b et c tels que a + b + c soit non nul, il existe un unique point G tel que

appelé barycentre du système pondéré {(A,a);(B,b);(C,c)}. Les points G, A, B et C sont toujours coplanaires et on démontre que , si A, B, C définissent un plan, tous les points M de ce plan peuvent s'écrire comme barycentre de A, B et C. Les pondérations s'appellent alors coordonnées barycentriques de M dans le repère A, B et C

Comme pour le barycentre de deux points, le barycentre de trois points permet de réduire l'expression vectorielle , pour tout point M :

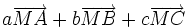
Ce qui permet, en remplaçant M par l'origine du repère, de donner les coordonnées du point G

Ce barycentre possède en outre une propriété dite d'associativité ou de barycentre partiel : si a + b est non nul et si G₁ est le barycentre du système {(A,a);(B,b)}, alors G est le barycentre du système {(G₁,a + b);(C,c)}. Cela signifie que la construction du barycentre de trois points peut se ramener à la construction de barycentres de deux points.

Cette propriété simplifie grandement les problèmes d'alignement et de concours.

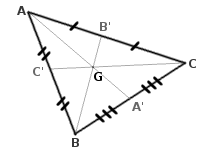
En considérant ces trois points comme les sommets d’un triangle, le centre de gravité est le point d'intersection de ses 3 médianes. Le centre de gravité est situé aux d'une médiane en partant du sommet.
Autrement dit, soit un triangle ABC, A' le milieu de [BC], B' le milieu de [AC], et C' le milieu de [AB] et G son centre de gravité.

Alors : , et .

Le centre de gravité est aussi l' isobarycentre des sommets du triangle, c'est-à-dire que .