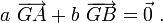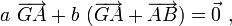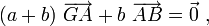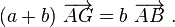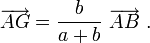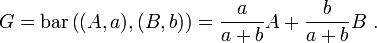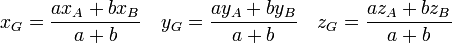Barycentre (géométrie élémentaire) - Définition

Introduction

En géométrie, le barycentre est un point qui permet de résumer un ensemble géométrique sur lequel sont réparties des valeurs numériques. Ces valeurs peuvent représenter des poids pour déterminer le point d'équilibre d'un mobile. Mais le barycentre permet aussi de caractériser le centre d'inertie d'un solide ou concentrer un ensemble de charges électriques.

Mathématiquement, le barycentre s'obtient en annulant une relation vectorielle. Cette notion généralise la construction du milieu d'un segment ou du centre de gravité d'un triangle.

Barycentre de deux points

Point d'équilibre

Le terme de barycentre est formé sur la racine grecque barus (lourd) pour désigner un centre des poids ou centre d'équilibre. Sa conception est liée au théorème des moments découvert par Archimède au III^e siècle av. J.-C.

Pour que la balance soit en équilibre, il faut que les moments, c'est-à-dire les produits des longueurs de bras par les masses correspondantes, soient égaux. Autrement dit le point d'équilibre est caractérisé par la relation : .

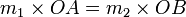
Par exemple, si la masse m₁ est 4 fois plus importante que la masse m₂, il faudra que la longueur OA soit 4 fois plus petite que la longueur OB.

Ce principe des moments est d'ailleurs utilisé dans la balance dite romaine

Les poids peuvent également avoir une valeur numérique négative, si l'une des masses est remplacée par un ballon d'hélium, par exemple. Dans ce cas, le point d'équilibre se situe en dehors de l'espace délimité par les deux objets.

Relation vectorielle

En géométrie affine, le point d'équilibre, ou barycentre, est noté G et les poids des points fixes A et B sont notés usuellement a et b. Le théorème des moments est remplacé par la relation

À l'aide de la relation de Chasles, cette relation peut se réécrire sous la forme

c'est-à-dire

ou de manière équivalente

Si la somme a + b est non nulle, il existe un unique point G qui satisfait cette équation. Il est donné par la relation

Cette relation est parfois notée (toujours sous l'hypothèse que a + b est non nul) :

Elle traduit alors la phrase « G est le barycentre des points A et B, affectés respectivement des coefficients a et b » .

Colinéarité

De la définition , on tire que ou encore que ; ainsi et sont colinéaires et ont un point en commun, G. Par conséquent, G appartient à la droite (AB). Nous venons de démontrer que

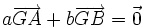
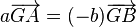
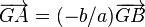
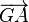
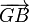
si G est le barycentre de {(A,a),(B,b)} alors G appartient à la droite (AB).

Si G est sur le segment [AB] (entre A et B) alors et sont de sens opposé, ce qui se traduit par avec k< 0. Mais, comme dans le même temps , on en déduit que b et a sont de même signe. Nous venons de démontrer que

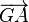
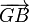
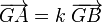
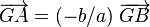
Si G est sur le segment [AB] (entre A et B) alors a et b sont de même signe.

Coordonnées barycentriques

On démontre (à démontrer ultérieurement) que, si A et B sont distincts, tout point M de la droite (AB) peut s'écrire comme barycentre des points A et B. Les pondérations obtenues sont appelées les coordonnées barycentriques du point M.

Homogénéité

Si G est le barycentre de {(A,a);(B,b)} alors, , et il vient que pour tout réel k . Autrement dit, on obtient De plus, comme a + b est non nul, pour tout k réel non nul, k(a + b) est également non nul. Alors G est le barycentre de {(A,k.a);(B,k.b)}.

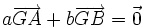
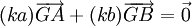
Nous venons de démontrer que

si G est le barycentre de {(A,a);(B,b)} alors pour tout k réel non nul, G est aussi le barycentre de {(A,ka);(B,kb)}.

Cette propriété s'appelle l'homogénéité.

Réduction

L'application de la relation de Chasles à , en introduisant le barycentre G de (A,a),(B,b) donne

.

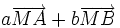
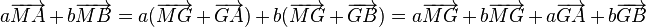
G étant barycentre de (A,a),(B,b) alors . La relation précédente devient:

.

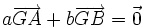
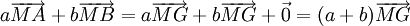
Nous venons de démontrer que

si G est le barycentre de (A,a),(B,b) alors pour tout M du plan,

.

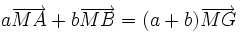
C'est la propriété de réduction.

Elle permet de positionner le point G par rapport à tout point M. Si M est l'origine d'un repère du plan ou de l'espace, elle permet de définir les coordonnées du point G