Base (arithmétique) - Définition

Symboles utilisés

Pour les bases jusqu'à 10 inclus, on utilise les chiffres 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9.

Au-delà, on utilise les lettres. Par exemple, pour la base 16, les symboles utilisés sont 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

L'usage du zéro positionnel est une convention pratique et élégante, mais non nécessaire pour représenter les entiers naturels, comme l'illustre le système décimal sans zéro. Il est, par contre, indispensable pour généraliser l'écriture positionnelle aux nombres fractionnaires.

Conversion d'une base (comprise entre 2 et 10) à une autre (comprise entre 2 et 10) - Pseudo-Code

      N:=NombreAConvertir      D:=0      I:=1      SI BaseDeDepart < 2 OU BaseDeDepart > 10 OU BaseDArrivee < 2 OU BaseDArrivee > 10 ALORS-FAIRE        RENVOYER "Avec ce pseudo-code, les 2 bases doivent être comprises ici entre 2 et 10"        STOP      SINON-FAIRE        TANT QUE N<>0 FAIRE:          D:= D + I*(N mod BaseDArrivee)          N:= N / BaseDArrivee          I:= I*BaseDeDepart        RENVOYER      FIN-du-test-SI (avec l'instruction SINON) concernant les 2 bases      

Avec "/" une division entiere (ex : 3/2=1), BaseDeDepart la base de NombreDeDepart et BaseDArrivee la base voulue.

Conversion d'une base à une autre

Un nombre dans une base n donnée s'écrit sous la forme d'additions des puissances successives de cette base.

• Le nombre c_n...c₂c₁c₀ en base b, constitué des chiffres c_n, ..., c₂, c₁, c₀, peut aussi s'écrire sous la forme c_nbⁿ + ... + c₂b² + c₁b¹ + c₀b⁰, c'est-à-dire un polynôme dont les coefficients sont les chiffres et l'inconnue est la base.

Lorsqu'on veut passer d'une base à une autre, on utilisera 2 méthodes (algorithmes) suivant que l'on sait calculer dans la base de départ ou dans la base d'arrivée.

Si on sait calculer dans la base de départ, des divisions entières successives par la base donneront en reste les chiffres du résultat, en commençant par les unités. Plus précisément :

q₀: = n (le nombre à convertir) ; i: = 0;

tant que q_i > 0 faire

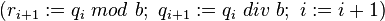
les r_i sont les chiffres du nombre converti, en partant des unités.

Si on sait calculer dans la base d'arrivée, on évalue le polynôme (en représentant les coefficients et la base de départ dans la base d'arrivée). La méthode de Horner est généralement utilisée :

v: = c_n  ; i: = n;

pour i:=n-1 a 0 faire v: = v * b + c_i ;

v est le nombre dans la base d'arrivée.

Si on ne sait calculer ni dans la base de départ ni dans celle d'arrivée, on passe par une base intermédiaire où l'on sait calculer.

Si la base d'arrivée est une puissance de la base de départ (exemple : de la base 2 à la base 16), on peut convertir groupes de chiffres à chiffre, localement et directement.

Bases non standard

On peut également employer des bases :

• négatives, pour lesquelles, comme pour les systèmes balancés, les nombres sont signés ;
• non-entières, on parle alors de bêta-numération (la base d'or en est un exemple) ;
• imaginaires (par exemple, le système quater-imaginaire ou la base , dans laquelle tout nombre complexe peut se développer, est une généralisation aux complexes du développement binaire) ;
• ...

Systèmes balancés

Un système numérique de base 2N ou 2N+1 peut également être doté des 2N+1 chiffres signés N, ..., 2, 1, 0, 1, 2, ..., N. On parle alors de système balancé.

Culture

• Le nombre π est irrationnel et donc, quelle que soit la base naturelle utilisée, les chiffres après la virgule sont infinis et ne présentent pas de répétition, au contraire des fractions comme 1/7 = 0.142857 142857...
• Boby Lapointe avait imaginé un usage comique du système hexadécimal, qu'il avait baptisé Système bibi-binaire.
• La RFC 1924 propose la base 85 pour la notation des adresses IPv6, mais ce n'est qu'un poisson d'avril.
• Dans le jeu vidéo Portal, lors du combat final, GlaDOS annonce que 2+2 font 10, avant de se rattraper en complétant avec "En base 4, tout va bien !".