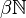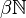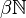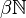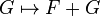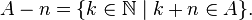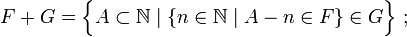Compactification de Stone??ech - Définition
La liste des auteurs de cet article est disponible ici.
Propriété universelle et fonctorialité
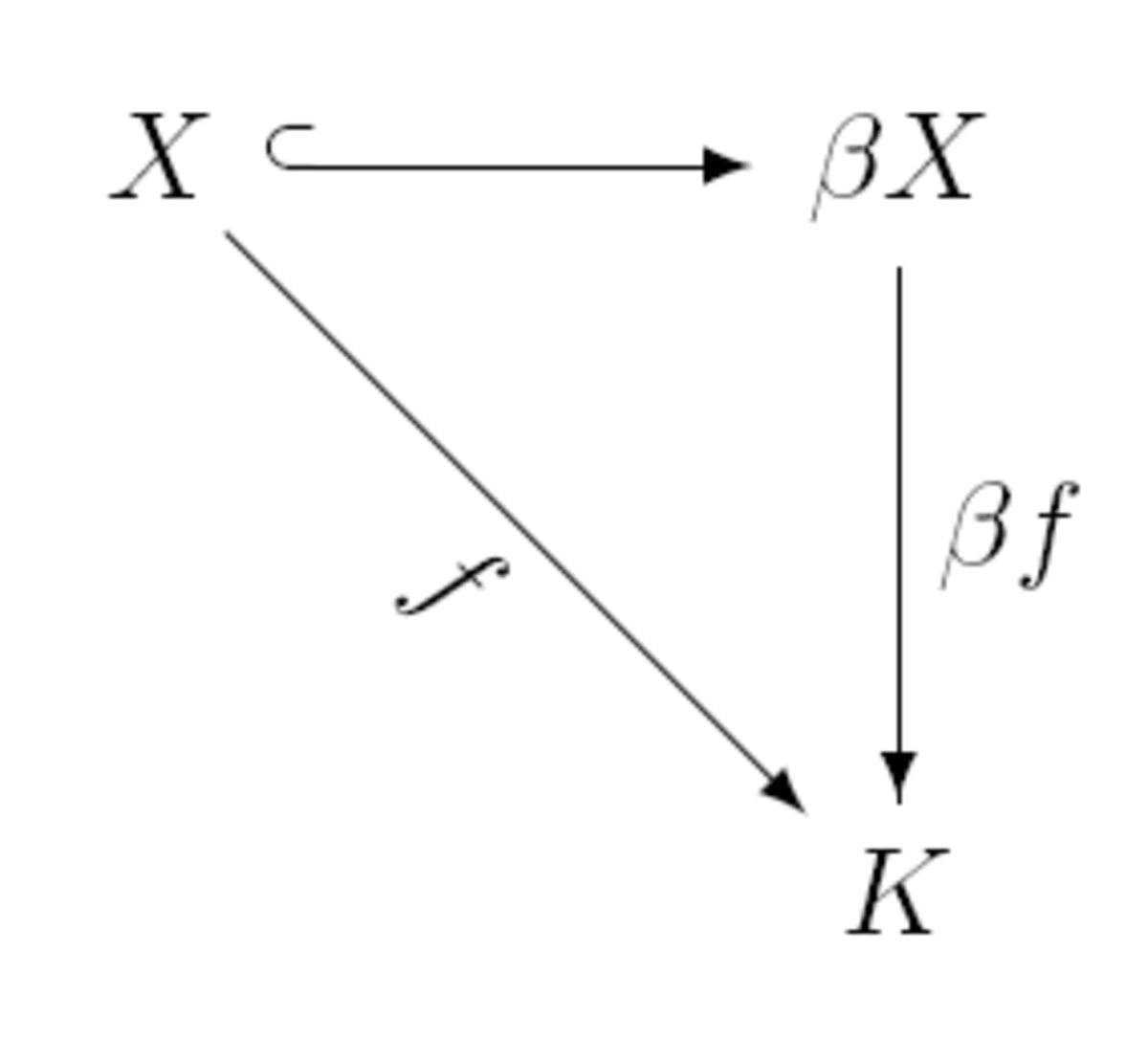
La définition précédente est un exemple de propriété universelle : elle affirme qu'il existe un morphisme βf unique rendant le diagramme suivant commutatif
Comme c'est le plus souvent le cas pour les propriétés universelles, cette propriété et le fait que βX soit compact caractérisent βX à un homéomorphisme près.
Certains auteurs demandent de plus que X soit un espace de Tychonov, ou même un espace localement compact, pour les raisons suivantes :
- L'application allant de X vers son image dans βX est un homéomorphisme si et seulement si X est un espace de Tychonov.
- Cette application est un homéomorphisme vers un sous-espace ouvert de βX si et seulement si X est un espace localement compact.
La construction de Stone–Čech peut être effectuée pour des espaces X quelconques, mais l'application X → βX n'est alors pas un homéomorphisme, et peut même ne pas être injective.
La propriété d'extension des applications fait de β un foncteur allant de Top (la catégorie des espaces topologiques) vers CHaus (la catégorie des espaces compacts). Si nous notons U le foncteur d'inclusion (qui est un foncteur d'oubli) de CHaus vers Top, les applications de βX vers K (pour K dans CHaus) correspondent bijectivement aux applications de X vers UK (en considérant leur restriction à X et en utilisant la propiété universelle de βX). Autrement dit, Hom(βX,K) = Hom(X,UK), ce qui veut dire que β est adjoint à gauche de U. Ceci entraîne que CHaus est une sous-catégorie réflexive de Top, avec β comme réflecteur.
Le cas des entiers naturels
La compactification de Stone–Čech des entiers naturels
Dans le cas où X est localement compact, par exemple


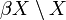

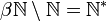
On peut voir
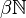

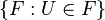
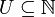

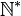
L'étude de βN, en particulier de
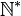
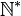
- Tout compact admettant une base formée d'au plus
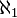
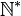
- En admettant l'hypothèse du continu,
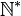
Ces résultats furent d'abord démontrés en considérant des algèbres de Boole et en utilisant la dualité de Stone.
Application : l'espace dual de l'espace des suites réelles bornées
Le compactifié βN peut être utilisé pour caractériser
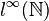
Étant donné une suite bornée
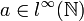


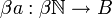
Cette extension est donc une application de l'espace des suites (de scalaires) bornées vers l'espace des fonctions continues allant de
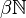
-
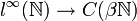
Cette application est bijective, puisque toute application de
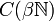
Ainsi,
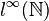
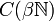
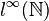
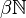
Enfin, il faut remarquer que cette technique se généralise à l'espace
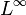
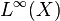
L'addition dans le compactifié de Stone–Čech des entiers
Les entiers (positifs) forment un monoïde pour l'addition. Il se trouve que cette opération peut être prolongée (mais non de manière unique) à
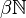
Pour tout sous-ensemble
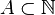
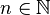
Étant donnés deux ultrafiltres F et G sur

cet ensemble est encore un ultrafiltre, et l'opération + est associative (mais non commutative) sur