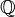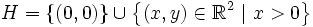Espace localement compact - Définition
En topologie, un espace localement compact est un espace qui, à défaut d'être compact, admet des voisinages compacts pour tous ses points. On peut y généraliser (au moins partiellement) beaucoup de résultats sur les espaces compacts. Ce sont aussi les espaces qu'on peut " rendre " compacts avec un point grâce à la compactification d'Alexandroff.
Motivations
La compacité est une source très fertile de résultats en topologie mais elle reste une propriété très contraignante. En particulier, le fait qu'un espace métrique doit être borné pour être compact fait que les résultats concernant les espaces compacts ne sont presque jamais applicables aux espaces métriques rencontrés, qui sont très rarement bornés.
Cependant on peut appliquer ces résultats à certains espaces métriques (et notamment les espaces vectoriels normés) non bornés à condition que l'objet étudié respecte certaines propriétés supplémentaires, qui permettent d'y appliquer les outils développés pour les espaces compacts.
Par exemple, toute suite de points d'un compact admet une valeur d'adhérence ; le théorème de Bolzano-Weierstrass dit qu'une suite de points de
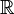
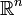
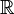
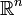
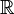
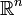

Autre exemple, peut-être plus parlant : un théorème connu dit que si une fonction est une bijection continue d'un espace compact vers un autre, alors sa réciproque est aussi continue (et donc c'est un homéomorphisme). C'est faux en général pour un espace topologique mais dans le cas de
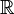
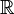
Le fait que ces deux résultats typiques de la compacité s'adaptent partiellement dans le cas d'espaces non compacts tient justement à la notion de compacité locale.
Espaces localement compacts
Définitions
Un espace topologique
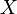
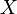
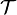
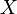
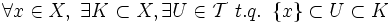
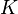
Cette définition implique immédiatement la caractérisation suivante (parfois prise comme définition) : un espace topologique
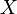
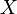
On note que dans ces définitions le mot " compact " peut être remplacé par exemple par " connexe " ou " connexe par arcs " pour obtenir d'autres notions ; c'est le procédé de définition des espaces " localement truc ". Voir Espace localement connexe, Espace localement connexe par arcs.
Propriétés
La première propriété des espaces localement compacts, la plus évidente, est que si un espace
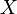
Comme la plupart des propriétés topologiques, la compacité locale est conservée par homéomorphisme : si
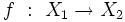
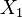
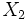
Un sous-espace
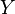
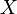
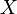
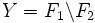
En particulier tous les ouverts et les fermés d'un espace localement compact
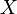
- Si
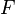
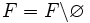
- Si
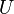
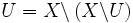
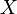
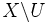
Un espace localement compact est un espace de Baire, c'est-à-dire que la conclusion du théorème de Baire s'y applique : une union dénombrable de parties nulle part denses (c'est-à-dire dont l'intérieur de l'adhérence est vide) est d'intérieur vide.
Exemples
L'ensemble des nombres réels
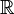
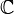
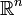
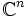
![]0,1[ \,\!](https://static.techno-science.net/illustration/Definitions/autres/e/e8390435831cf41fa3844f71e0096765_9885e51f20835d2bbb4418d6ccb5e1c9.png)
En revanche, l'ensemble des nombres rationnels