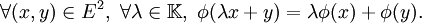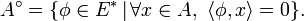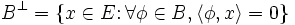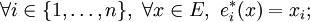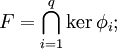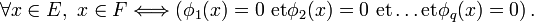Espace dual - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, l'espace dual d'un espace vectoriel E est l'ensemble des formes linéaires sur E.
La structure d'un espace et celle de son dual sont très liées. La fin de cet article présente quelques résultats sur les liens entre espace dual et hyperplans, ce qui permet une compréhension « géométrique » de certaines propriétés des formes linéaires.
Le dual topologique est une variante très considérée en analyse fonctionnelle, lorsque l'espace vectoriel est muni d'une structure additionnelle d'espace vectoriel topologique.
Définitions
Soient
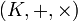
On appelle forme linéaire sur E toute application linéaire de E vers K, c'est-à-dire toute application
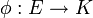
L'ensemble
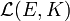
Si φ est un élément de E * et x un élément de E, on écrit parfois
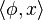
Exemples
Cas d'un espace préhilbertien
Si l'espace vectoriel E est un espace préhilbertien réel, c'est-à-dire muni d'un produit scalaire
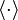
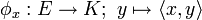
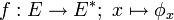
Orthogonal
Ici, E est un espace vectoriel quelconque (on ne suppose pas de dimension finie).
Si A est un sous-espace de E, on définit l'orthogonal
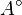
Si B est un sous-espace de E * , on définit l'orthogonal
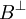
Il ne faut pas confondre la notion d'orthogonal d'un sous-espace dans la théorie de dualité avec l'orthogonalité dans la théorie des espaces euclidiens.
Dualité en dimension finie
Si l'espace E est de dimension finie n, alors l'espace dual E * , isomorphe à E, est lui aussi de dimension n. On peut raffiner ce résultat.
Théorème de la base duale — Soit
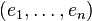
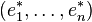
(où xi est la coordonnée de x correspondant au vecteur ei) définit une base de E * , appelée base duale. Et par construction, on a
- dimE = dimE * .
En dimension finie, un espace a donc la même dimension que son espace dual. Remarquons que d'après le Théorème de Erdös-Kaplansky, ceci est faux pour tout espace vectoriel de dimension infinie
Exemple
Les polynômes de Lagrange associés à des scalaires
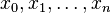
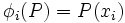
Représentation des sous-espaces
Ce paragraphe présente une application très importante de l'étude de l'espace dual : la représentation d'un sous-espace comme intersection d'hyperplans. On se restreint ici au cas d'un espace vectoriel de dimension finie.
Soit E un K-espace vectoriel de dimension finie n.
Soit F un sous-espace de dimension p (distinct de E) ; on a donc p < n.
Alors, il existe q = n − p formes linéaires indépendantes
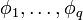
c'est-à-dire
Ce théorème généralise les résultats élémentaires connus en dimension 2 ou 3 sur la représentation de droite ou de plan par des équations. En particulier, dans un espace vectoriel de dimension 3, l'intersection de 2 plans indépendants est une droite.
Nota : il ne faut pas confondre la notion de droite ou de plan dans un espace affine (qui correspond à l'intuition géométrique) et celle, utilisée ici, de droite vectorielle ou de plan vectoriel. On appelle droite vectorielle un sous-espace de dimension 1, et plan vectoriel un sous-espace de dimension 2.
On peut donc représenter un sous-espace F de dimension p par q équations linéaires indépendantes, où
- q = dimE − p.