Compactification de Stone??ech - Définition

Introduction

En mathématiques, et plus précisément en topologie générale, la compactification de Stone–Čech (découverte en 1937 par Marshall Stone et Eduard Čech) est une technique de construction d'un espace compact prolongeant un espace topologique donné X ; plus précisément, il s'agit de la construction d'une application universelle allant de X vers un espace compact βX.

Définition

Le compactifié de Stone–Čech, βX, d'un espace topologique X est le plus grand compact "engendré" par X. Plus rigoureusement :

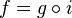
On verra dans les sections suivantes que le couple (i,Y) est essentiellement unique (à unique isomorphisme près), et que l'axiome de choix permet de démontrer son existence pour tout espace topologique X. En revanche, X ne peut être considéré comme un sous-espace (dense) de βX (autrement dit i n'est un plongement) que si X est un espace de Tychonov ; i peut même ne pas être injective, elle le sera si et seulement si X est un espace d'Uryssohn.

Constructions

La section précédente a montré l'unicité (à homéomorphisme près) du compactifié de Stone–Čech. Les constructions équivalentes suivantes nécessitent toutes l'axiome de choix ; seules les deux premières s'appliquent à des espaces X généraux.

À l'aide de produits

Une tentative de construction du compactifié de Stone–Čech de X est de prendre l'adhérence de l'image de X dans , où le produit est pris sur l'ensemble de toutes les applications continues de X vers des espaces compacts C. Cette construction, sous cette forme, échoue, parce que cette collection d'applications est une classe propre et non un ensemble ; il est cependant possible de la rendre correcte, par exemple en restreignant les compacts C à l'ensemble des couples (Y,T), où Y=P(P(X)) (l'ensemble des parties de l'ensemble des parties de X), et où T est une des topologies rendant Y compact. Y est choisi suffisamment grand pour que son cardinal soit au moins égal à celui de tout compact vers lequel il existe une application continue f de X telle que f(X) soit dense.

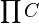
En utilisant l'intervalle unité

Considérons l'application F de X vers [0,1]^C, définie par

où C est l'ensemble de toutes les applications continues de X vers [0,1]. On voit que F est continue, si l'on munit [0,1]^C de la topologie produit. D'après le théorème de Tychonov, on sait que [0,1]^C est compact puisque [0,1] l'est, donc l'adhérence de F(X) dans [0,1]^C est une compactification de X.

Pour montrer qu'on obtient bien le compactifié de Stone–Čech , il faut contrôler la propriété universelle. On le vérifie d'abord pour K = [0,1], où l'extension cherchée de f : X → [0,1] est la projection sur la "f-ème"" coordonnée dans [0,1]^C. pour généraliser cela à un compact K quelconque, on remarque que K peut être plongé dans un cube (un produit de la forme [0,1]^I), on étend comme précédemment chacune des fonctions coordonnées, et on prend le produit de ces extensions.

Cette construction réussit parce que l'intervalle unité est un cogénérateur de la catégorie des espaces compacts : cela veut dire que si f et g sont deux applications (continues) distinctes entre deux compacts A et B, il existe une application h de B vers [0,1] telle que hf et hg sont distinctes. Tout autre cogénérateur pourrait ëtre utilisé pour la même construction.

À l'aide d'ultrafiltres

Si X est discret, on peut construire βX comme l'ensemble de tous les ultrafiltres sur X, muni de la topologie dite topologie de Stone. X est identifié au sous-ensemble de βX formé des ultrafiltres triviaux.

Pour vérifier la propriété universelle dans ce cas, on remarque que pour f : X → K avec K compact et F un ultrafiltre sur X, on a un ultrafiltre f(F) sur K, qui converge vers un élément (unique) x, puisque K est compact ; on définit alors βf(F) = x, qui est une extension continue de f pour la topologie de Stone.

Cette construction est équivalente à celle de l'espace de Stone (en) construit sur l'algèbre de Boole de l'ensemble des parties de X, et peut être généralisée à des espaces de Tychonov arbitraires en utilisant des filtres maximaux d'ensembles de zéros de fonctions continues de X vers R, ou simplement des filtres maximaux de fermés si l'espace est normal.

En utilisant des C*-algèbres

Dans le cas où X est complètement régulier, le compactifié de Stone-Čech peut être identifié avec le spectre de C_b(X), la C*-algèbre de l'ensemble des fonctions continues bornées sur X munie de la norme sup.