Compter sur ses doigts - Définition

Les opérations

La retenue

Une numération avec la main permet de mémoriser la retenue d'une opération. Dans ce cas, Il est fréquent d'indiquer la valeur numérique en appuyant un doigt sur une partie du corps (menton, front, crâne) ou sur la table de travail.

La multiplication par 9

Méthode 1

Pour multiplier rapidement par 9 avec ses mains, il faut ouvrir ses 10 doigts, puis baisser le doigt correspondant au nombre multiplié, les doigts restants à gauche du doigt plié correspondent aux dizaines, ceux à droite aux unités.

Par exemple 9 x 6 :

on plie le pouce droit, il reste les 5 doigts de la main gauche : 50 ( 5*10); et les 4 doigts de la main droite : 4 (4*1). Ainsi

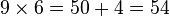
Méthode 2

On peut également procéder ainsi :

9 x 6
(6-1)=5
(10-6)=4

Ce qui permet de trouver 54 ; en effet, on voit que :

09
18
27
36
45
54
63
72
81
90

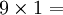
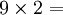
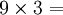
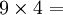
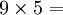
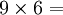
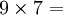
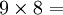
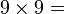
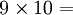
On constate que les chiffres des dizaines se suivent dans l’ordre croissant et ceux des unités dans l’ordre décroissant…

La méthode mathématique

Ces méthodes, démontrées mathématiquement, permettent presque d'atteindre facilement 4¹⁰ avec deux mains. Cependant, elles sont inutilisables telles quelles, les calculs (changements de bases) étant souvent bien compliqués...

Un système binaire

Les doigts peuvent, basiquement, adopter deux positions : levé ou fermé, ce qui fait deux états. Soit 0 l'état "fermé" et 1 l'état "levé" : on se retrouve dans le cas d'un nombre binaire. Avec 10 doigts, en adoptant le code binaire, on pourrait donc compter jusqu'à :

2¹⁰ − 1 = 1023

L'inconvénient étant le sens de lecture, on peut tenir une main dans un sens (vers l'interlocuteur) pour les valeurs les plus basses (less significant bits) et dans un autre sens (vers soi) pour les valeurs les plus élevées (most significant bits).

Dans ce cas, si la main gauche est vers soi et que la main droite est dans l'autre sens, le pouce gauche levé représente 512, pouce droit levé représente 1. Les deux mains ouvertes représentent 1023.

Voir Système binaire

Un système plus poussé

Il est possible d'aller encore plus loin dans la numération. D'une part, on peut utiliser les phalanges, qui permettent aux doigts de se plier, pour obtenir 4 états : levé, plié, fermé, fermé et tendu - à causes des limitations anatomiques de l'annulaire, les doigts "pliés" doivent toucher la base du doigt, les doigts "fermés" doivent toucher la paume de la main (comme lorsqu'on serre le poing). Ici, la numération se ferait en base 4, et on pourrait compter jusqu'à :

4¹⁰ − 1 = 1048575

Plus encore, on pourrait utiliser la position des mains et éventuellement les croisements de doigts, voire des méthodes encore plus développées : une multiplication pour approcher le nombre, suivie d'une addition ou d'une soustraction pour ajuster et avoir le résultat exact - il suffit pour symboliser les opérations d'indiquer avec l'index des deux mains un + ou un × ou un -.

Bien évidemment, ces méthodes demandent de la part de leurs pratiquants de grandes capacités de calcul mental - et sont donc presque inutilisables. Cependant, si on dispose d'une grille répertoriant les positions des doigts et les chiffres représentés, alors il devient aisé de développer ce genre de techniques, au moins pour la méthode simple (binaire).