Connexité (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Connexité et nombres réels
Montrons que les parties connexes de
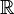
- Si A est une partie connexe de
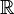
![]-\infty,a[\cap A](https://static.techno-science.net/illustration/Definitions/autres/2/28b931a7fb81c12ade28d7153fc5b78e_8d724d57e12d66502cc28bd192b8eb85.png)
![]a,+\infty[\cap A](https://static.techno-science.net/illustration/Definitions/autres/c/c4c922e130d59f0cd8f2b7e72e062111_9bcbe9763d7ef9e0fa4a7af3c06e12b1.png)
- Si A est un intervalle de
Deux applications fondamentales à l'Analyse
Pour montrer qu'une propriété est vraie pour tous les points d'une partie que l'on sait connexe, on montre que l'ensemble des points qui la satisfait est ouvert et fermé. C'est ce qu'on fait pour le théorème d'unicité global des solutions d'une équation différentielle, et pour le principe du prolongement analytique.
Applications localement constantes
Définition
Soit X un espace topologique, et Y un espace séparé (par exemple un espace métrique).
Une application f de X dans Y est dite localement constante sur X si pour tout
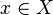
Une fonction localement constante sur X n'est pas forcément constante sur X. Intuitivement, c'est le cas si l'ensemble X est « en un seul morceau », ce que montre le théorème suivant
Théorème
Si X est connexe, toute application localement constante sur X est constante.
Applications à la topologie
Les applications sont nombreuses. La droite

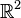
Le même argument montre que le cercle S1 n'est pas homéomorphe à un intervalle.
Cet argument ne s'étend pas aux dimensions supérieures. Si on veut montrer en utilisant les mêmes idées que
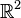
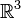
On peut encore citer, comme application de la connexité, l'analyse de l'énigme des trois maisons. l'objet de cet énigme est de relier trois points du plan identifiés à des maisons à trois autres, identifiés à des fournisseurs (eau, gaz et électricité). Chaque maison doit être reliée aux trois fournisseurs et les liens ne doivent pas se croiser. La démonstration de l'impossibilité de résolution se fonde sur le théorème de Jordan, qui s'exprime en termes de connexité.

















































