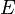Connexité (mathématiques) - Définition

Introduction

Un archipel, comme celui des îles Canaries, n'est pas connexe : il n'est pas possible de passer à pied sec d'une île à l'autre. Les îles sont les composantes connexes de l'archipel.

La connexité est une notion de topologie qui formalise le concept d'« objet d'un seul tenant ». Un objet est dit connexe s'il est fait d'un seul « morceau », dans le cas contraire, chacun des morceaux est une composante connexe de l'objet étudié.

Définition

L'espace vert A est connexe, alors que l'espace bleu B ne l'est pas

Soit un espace topologique E. Les quatre propositions suivantes sont équivalentes :

• E n'est pas la réunion de deux ouverts non vides disjoints ;
• E n'est pas la réunion de deux fermés non vides disjoints ;
• Il n'existe pas dans E de sous-ensemble à la fois ouvert et fermé distinct du vide et de E ;
• Toute application continue de E dans un ensemble à deux éléments muni de la topologie discrète est constante.

Cette dernière caractérisation est souvent la plus commode à utiliser pour démontrer un résultat de connexité.

Dans le cas où ces conditions sont remplies on dit que l'espace E est connexe.

Une partie X d'un espace topologique E est dite connexe si elle est un espace connexe lorsqu'elle est munie de la topologie induite.

Propriétés

Union, intersection, adhérence

Exemples d'unions et d'intersections connexes ou non.

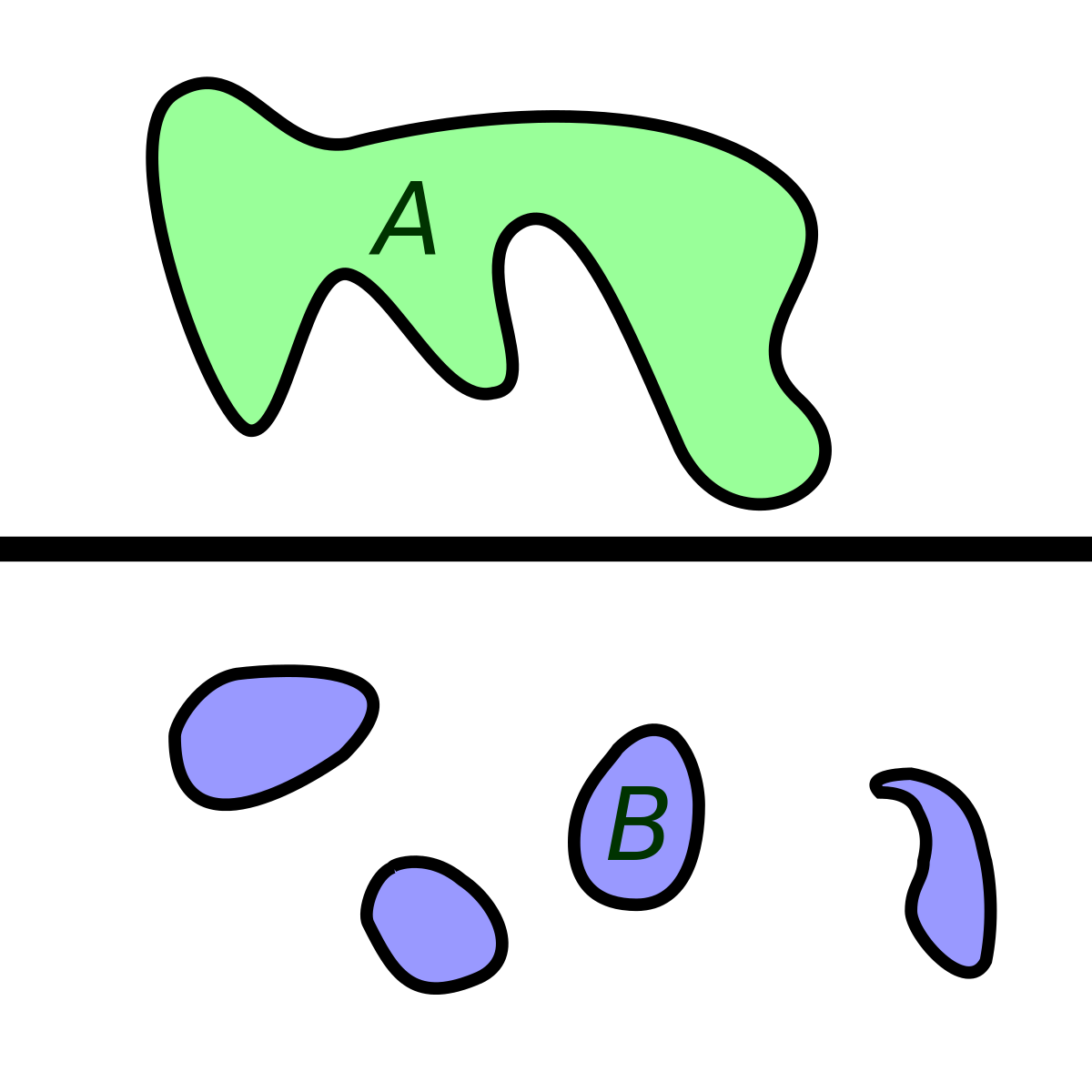
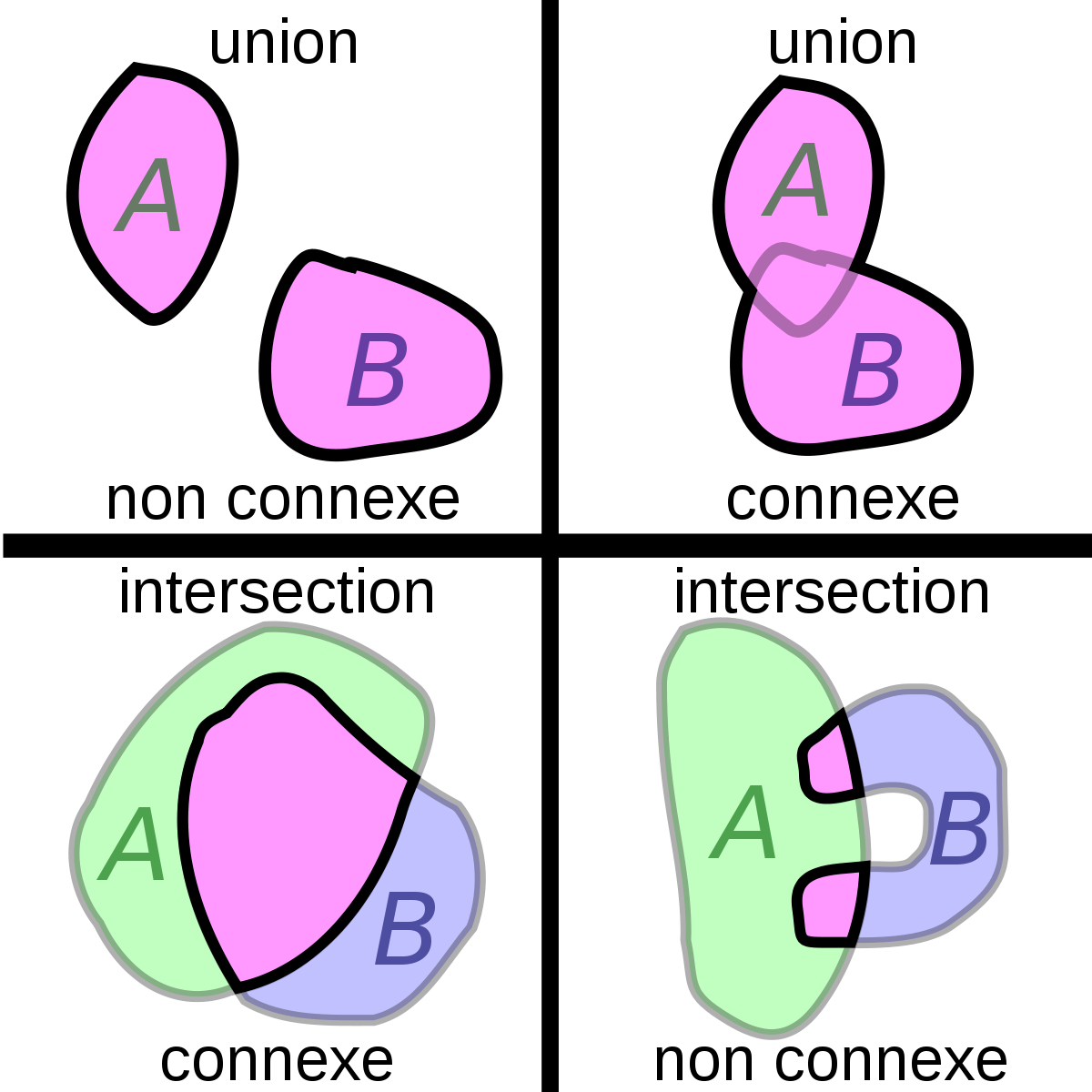
Si X et Y sont deux parties connexes d'un espace topologique E, en général l'union et l'intersection de X et Y ne sont pas connexes.

En revanche, l'union des deux parties connexes est connexe si elles ont un point commun. Plus généralement, si est une suite de parties connexes telle que chacune a un point commun avec la suivante : alors la réunion est connexe.

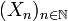
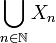
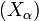
Autre généralisation : la réunion d'une famille quelconque de parties connexes de E est connexe, si leur intersection est non vide. Exemple d'application : toute partie connexe par arcs est connexe.

Si est connexe, toute partie B telle que est connexe (on a désigné par l'adhérence de A , qui dans ce cas est donc aussi connexe ).

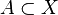
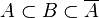
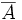
Composantes connexes

Étant donné un point dans un espace topologique , la réunion de toutes les parties connexes contenant est connexe. C'est la plus grande (au sens de la relation d'inclusion) de toutes les parties connexes contenant . On la note et on l'appelle composante connexe de dans . Les composantes connexes sont des parties fermées.

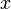
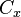
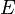
Au minimum, on a C_x = {x} ; cela signifie que {x} est le seul sous-ensemble connexe de E contenant x mais pas forcément que x est un point isolé (cf. exemples). Si cette propriété est vraie pour tout x, on dit que l'espace est totalement discontinu. Au maximum, on a C_x = E ; c'est le cas où E est connexe.

On définit une relation d'équivalence sur E de la manière suivante : on dit que x et y sont connectés si et seulement si . Cette relation équivaut à . Les classes d'équivalence pour cette relation sont les composantes connexes de E ; ainsi tout espace topologique se décompose en union disjointe de parties connexes maximales pour l'inclusion (il n'y en a qu'une si l'espace est connexe !)

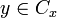
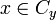
Exemples :

• a deux composantes connexes : et .
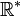
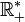
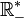
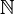
• Dans et plus généralement dans un espace muni de la topologie discrète, les composantes connexes sont les singletons.
• Dans aucun point n'est isolé, mais les composantes connexes sont aussi les singletons. Le même phénomène se produit pour l'ensemble de Cantor.
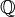
• Le groupe des matrices inversibles de taille n a deux composantes connexes, données par le signe du déterminant.

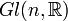
Connexité et continuité

D'après la définition, un espace E est connexe lorsque l'image de E par une application continue n'est jamais un ensemble à deux éléments muni de la topologie discrète. Or une telle paire est non connexe.

En fait, on peut démontrer plus généralement que l'image d'un espace connexe par une application continue est toujours connexe. Plus précisément si est un espace connexe, un espace topologique et une application continue, alors est une partie connexe de .

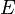
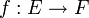
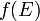
Ceci est une généralisation du théorème des valeurs intermédiaires, qui correspond au cas où est un intervalle de et où .