Corps (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Corps et anneau
L'ensemble
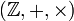
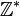
Plus généralement, un ensemble A muni de deux lois + et × vérifiant
- (A, +) forme un groupe commutatif dont l'élement neutre est noté 0
- (A-{0}, ×) forme un monoïde.
- la multiplication est distributive pour l'addition (à gauche comme à droite)
est un anneau unitaire.
Si l'anneau A est intègre, c’est-à-dire si
-
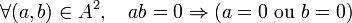
ou encore,
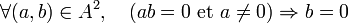
l'anneau est presque un corps car il ne lui manque plus que l'inversibilité pour la multiplication.
- On démontre que si l'anneau A est commutatif intègre, on peut le plonger dans son corps des fractions, qui est le plus petit corps contenant l'anneau.
Exemple :

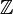
Un anneau intègre (unitaire) est un corps si et seulement si {0} et A (les idéaux triviaux) sont les seuls idéaux.
Un anneau intègre (unitaire) A est un corps si et seulement si tout A-module est libre.
Corps finis
Ce sont les corps dont le nombre d'éléments est fini. L'étude des corps finis est tardive dans l'étude des corps. On démontre qu'un corps fini est toujours commutatif, de cardinal égal à la puissance d'un nombre premier. Il est en fait possible de dresser la liste de tous les corps finis (à isomorphisme près).
Le plus petit corps fini est celui des booléens, dont voici les tables d'addition et de multiplication:
| + | 0 | 1 | |
| 0 | 0 | 1 | |
| 1 | 1 | 0 |
| x | 0 | 1 | |
| 0 | 0 | 0 | |
| 1 | 0 | 1 |
Les corps finis les plus connus sont les corps de congruences modulo un nombre premier comme dans le cas ci-dessus, mais il en existe une infinité d’autres, comme par exemple ceux-ci, respectivement à quatre et neuf éléments, dont nous donnons ci-dessous les « tables de Pythagore », successivement pour la première loi de composition dite « addition », puis pour la deuxième dite « multiplication ». Nous désignons dans chaque cas comme a l’élément neutre de la première loi de composition, b celui de la deuxième.
Quatre éléments :
| + | a | b | c | d | |
| a | a | b | c | d | |
| b | b | a | d | c | |
| c | c | d | a | b | |
| d | d | c | b | a |
| x | a | b | c | d | |
| a | a | a | a | a | |
| b | a | b | c | d | |
| c | a | c | d | b | |
| d | a | d | b | c |
Neuf éléments :
| + | a | b | c | d | e | f | g | h | i | |
| a | a | b | c | d | e | f | g | h | i | |
| b | b | c | a | e | f | d | h | i | g | |
| c | c | a | b | f | d | e | i | g | h | |
| d | d | e | f | g | h | i | a | b | c | |
| e | e | f | d | h | i | g | b | c | a | |
| f | f | d | e | i | g | h | c | a | b | |
| g | g | h | i | a | b | c | d | e | f | |
| h | h | i | g | b | c | a | e | f | d | |
| i | i | g | h | c | a | b | f | d | e |
| x | a | b | c | d | e | f | g | h | i | |
| a | a | a | a | a | a | a | a | a | a | |
| b | a | b | c | d | e | f | g | h | i | |
| c | a | c | b | g | i | h | d | f | e | |
| d | a | d | g | c | f | i | b | e | h | |
| e | a | e | i | f | g | b | h | c | d | |
| f | a | f | h | i | b | d | e | g | c | |
| g | a | g | d | b | h | e | c | i | f | |
| h | a | h | f | e | c | g | i | d | b | |
| i | a | i | e | h | d | c | f | b | g |

















































