Corps (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Corps et équation algébrique
L'étude des polynômes à coefficient dans un corps commutatif et la recherche de leurs racines a développé considérablement la notion de corps. Si f est un polynôme de degré n sur un corps commutatif K, l'équation f(x) = 0 est une équation algébrique dans K. Si, de plus, f est un polynôme irréductible, l'équation est dite irréductible. Lorsque n ≥ 2, trouver les solutions d'une telle équation demande de se placer dans un corps plus grand que K, une extension de corps.
Par exemple, l'équation x2 − 2 = 0 est irréductible dans


![\mathbb Q[\sqrt 2]](https://static.techno-science.net/illustration/Definitions/autres/d/db51c502f6ea3908be57943d0ba5af9a_dba329edcc1e4263bb2ef895fe637c73.png)


![\mathbb Q[i]](https://static.techno-science.net/illustration/Definitions/autres/2/2830a273d48073b03c768cce92401ea7_554428f47abd215526a5674373f65046.png)
Un corps de rupture d'un polynôme est, par exemple, un corps minimal contenant K et une racine de f.
Le corps de décomposition de f est le plus petit corps contenant K ainsi que toutes les racines de f.
L'étude des corps de décomposition d'un polynôme et du groupe de permutations de ses racines forme la branche des mathématiques que l'on appelle la théorie de Galois.
Corps et espace vectoriel
Partant du corps



Autres champs d'étude
On retrouve la théorie des corps dans l'étude de certaines fonctions comme les fonctions rationnelles ou les fonctions elliptiques
Propriétés
- Soit
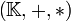

- Soit
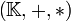
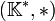
-
- Le nombre de racines d'un polynôme est inférieur ou égal à son degré.
L'anneau K[X] possède une division euclidienne, il est donc euclidien et par voie de conséquence factoriel (cf l'article anneau euclidien). Il est donc décomposable en produit de polynômes irréductibles. Si un polynôme irréductible P[X] n'est pas de degré 1, alors il n'admet pas de racine. En effet, si k est un élément du corps, la division euclidienne montre que le polynôme X - k divise tout polynôme ayant k pour racine. Le polynôme P[X], n'ayant pas de diviseur de degré 1, ne peut avoir de racine.
En conséquence, un polynôme quelconque admet autant de racines que sa décomposition en facteurs irréductibles contient de polynôme de degré 1, car un corps est intègre. Le fait qu'un produit de polynômes admet comme degré la somme des degrés des polynômes du produit permet de conclure.
-
- Tout sous-groupe fini du groupe multiplicatif est cyclique :
Soit G un tel sous-groupe, n son cardinal et e son exposant. L'exposant d'un groupe est le plus petit commun multiple des ordres des éléments du groupe. Le polynôme Xe - 1 admet chaque élément du groupe comme racine. Comme dans un corps commutatif, un polynôme n'admet jamais plus de racines que son degré, e est au moins égal à n. Le théorème de Lagrange montre que e est au plus égal à n et e est égal à n. Il existe toujours un élément g d'ordre l'exposant dans un groupe abélien fini (cf l'article exposant d'un groupe), en conséquence, g est d'ordre n et donc générateur du groupe G ce qui montre son caractère cyclique.

















































