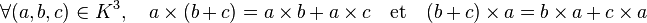Corps (mathématiques) - Définition

Introduction

En mathématiques, et plus précisément en algèbre, un corps est une structure algébrique. De manière informelle, un corps est un ensemble dans lequel il est possible d'effectuer des additions, des soustractions, des multiplications et des divisions.

Des exemples élémentaires de corps sont le corps des nombres rationnels (noté ), le corps des nombres réels (noté ), le corps des nombres complexes (noté ) et le corps des congruences modulo p où p est un nombre premier. L'exemple le plus simple de corps non commutatif (parfois appelés anneau à division, suivant l'anglais) est celui des quaternions.

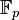
La théorie des corps est appelée, par certains, théorie de Galois ; cependant, la théorie de Galois désigne en général une méthode d'étude qui s'applique en particulier aux corps commutatifs et aux extensions de corps, qui forment l'exemple historique, mais s'étend aussi à bien d'autres domaines, par exemple l'étude des équations différentielles (théorie de Galois différentielle), ou des revêtements. Autrement dit, la théorie de Galois est une branche de la théorie des corps.

Fragments d'histoire

Jusqu'au XIX^e siècle, les ensembles de nombres ont paru tellement naturels que l'on ne s'est jamais préoccupé de leur donner un nom, ni même de définir avec précision leur structure. Cependant, avec la naissance de l'étude des nombres algébriques, il est apparu d'autres ensembles de nombres que les rationnels, les réels et les complexes. Il est devenu nécessaire de préciser la structure de corps, puis la notion d'entiers sur ce corps et enfin la notion d'anneau. C'est à l'école allemande que l'on doit le développement de ces notions. C'est Richard Dedekind qui définit pour la première fois la structure de corps (Körper en allemand) et c'est la raison pour laquelle un corps quelconque est souvent nommé K ou . La structure de corps s'insère dans une hiérarchie comprenant le monoïde, le groupe, l'anneau, et donne lieu à la définition de l'espace vectoriel, et de l'algèbre.

Caractéristique

S'il existe un entier naturel n non nul tel que (avec n termes) est nul, on appelle caractéristique du corps le plus petit entier positif non nul vérifiant cette propriété. S'il n'existe pas d'entier non nul vérifiant cette propriété, on dit que le corps est de caractéristique nulle (parfois aussi grande que l'on veut).

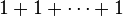
Par exemple le corps est de caractéristique nulle alors que le corps est de caractéristique p. On démontre qu'un corps possède toujours pour caractéristique soit 0 soit un nombre premier.

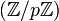
Définition et exemple

Un corps est un ensemble K muni de deux lois internes notées en général + et × vérifiant

• (K, +) forme un groupe commutatif dont l'élément neutre est noté 0
• (K \ {0}, ×) forme un groupe multiplicatif.
• la multiplication est distributive pour l'addition (à gauche comme à droite) c’est-à-dire que

On parle alors du corps (K, +, ×)

Les premiers corps étudiés étant des ensembles de nombres (rationnels, réels, complexes, algébriques), la multiplication y était commutative. C'est la raison pour laquelle, initialement, dans la définition d'un corps, la multiplication devait être commutative. Actuellement, la tendance est plutôt de ne pas exiger la commutativité de la multiplication ou du moins de préciser la nature des corps étudiés; on appelle alors corps commutatif un corps dont la multiplication est commutative. Les corps non commutatifs sont parfois appelés corps gauches ou anneaux à division. Cette terminologie est inspirée de l'anglais où un corps commutatif est appelé field et un corps non nécessairement commutatif division ring.

Exemples de corps

• L'ensemble des nombres rationnels, est un corps commutatif
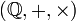
• L'ensemble des nombres réels est un corps commutatif
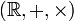
• L'ensemble des complexes est un corps commutatif
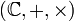
• L'ensemble des quaternions est un corps non commutatif
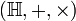
• En arithmétique modulaire, l'ensemble , où p est un nombre premier, est un corps commutatif.

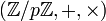
Un sous-corps d'un corps K est une partie non vide L de K, stable par et , telle que L munie des lois induites soit un corps.