Dualité de Pontryagin - Définition

La dualité de Pontryagin dans le cadre de la théorie des catégories

Il peut être utile de considérer le groupe dual fonctoriellement. Dans ce qui suit, GALC désigne la catégorie des groupes abéliens localement compacts et des homomorphismes de groupes continus. La construction du groupe dual G^{^} est un foncteur contravariant GALC → GALC. En particulier, le foncteur itéré G → (G^{^})^{^} est covariant.

Théorème. Le foncteur de dualié est un isomorphisme de catégories de la catégorie GALC vers sa catégorie opposée GALC^op.

Théorème. Le foncteur dual itéré est naturellement isomorphe au foncteur identité de GALC.

Cet isomorphisme peut se comparer à la construction du bidual d'un espace vectoriel de dimension finie.

Cette dualité échange les sous-catégories des groupes discrets et des groupes compacts. Si A est un anneau et G est un A-module à gauche, le groupe dual G^ devient un A-module à droite; de cette façon les A-modules à gauche discrets sont duaux au sens de Pontryagin des A-modules à droite compacts. L'anneau End(G) des endomorphismes dans GALC est par dualité envoyé sur son anneau anneau opposé. Si G est par exemple un groupe cyclique discret infini (isomorphe à ), G^ est un groupe circulaire (isomorphe au groupe ). L'anneau des endomorphismes du premier est , il en est donc de même du second.

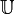
Bibliographie

Les ouvrages suivants possèdent des chapitres consacrés aux groupes abéliens localement compacts, la dualité et la transformée de Fourier. L'ouvrage de J. Dixmier possède aussi du matériel spécifique à l'analyse harmonique non commutative.

• Jacques Dixmier (en), Les C*-algèbres et leurs Représentations, Gauthier-Villars,1969.
• Lynn H. Loomis (de), An Introduction to Abstract Harmonic Analysis, D. van Nostrand Co, 1953
• Walter Rudin, Fourier Analysis on Groups, 1962
• Hans Reiter (de), Classical Harmonic Analysis and Locally Compact Groups, 1968 (2nd éd par Jan D. Stegeman, 2000).
• Hewitt (en) et Ross, Abstract Harmonic Analysis, vol 1, 1963.

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Pontryagin duality »