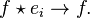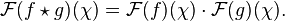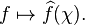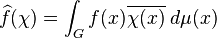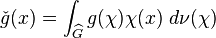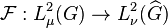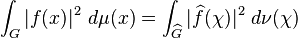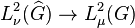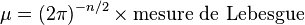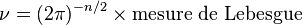Dualité de Pontryagin - Définition
La liste des auteurs de cet article est disponible ici.
Le groupe dual
Si G est un groupe abélien localement compact, un caractère de G est un morphisme de groupe continu de G dans
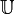
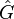
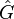
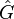
Théorème:
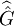
Canonique signifie qu'il y a une application "naturelle" de G dans
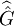
Autrement dit, chaque élément x de G est identifié à son évaluation par les caractères du dual.
Algèbre de groupe
L'espace des fonctions intégrables sur un groupe abélien localement compact G est une algèbre, où la multiplication est le produit de convolution: si f et g sont des fonctions intégrables alors leur produit de convolution est défini par
Théorème L'espace de BanachL1(G) est une algèbre associative et commutative muni de la convolution.
Cette algèbre est appelée l'algèbre du groupe G. Comme L1(G) est complet, c'est une algèbre de Banach. Elle ne possède pas d'élément neutre pour la multiplication, à moins que G soit un groupe discret.
Cette algèbre a cependant, en général, une approximation de l'unité {ei}i qui est un réseau (ou une suite généralisée) indexée par un ensemble inductif I, satisfaisant la propriété suivante
La transformée de Fourier transforme la convolution en multiplication, c'est-à-dire:
En particulier, à chaque caractère de G correspond une unique fonctionnelle multiplicative linéaire de l'algèbre du groupe définie par
Ce fait constitue une propriété importante des algèbre de groupes : en effet on peut alors expliciter les fonctionnelles multiplicatives linéaires non nulles de l'algèbre du groupe.
Transformée de Fourier
Le groupe dual d'un groupe abélien localement compact sert comme espace de base d'une version plus abstraite de la transformée de Fourier. Si
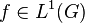
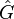
où l'intégrale est prise par rapport à la mesure de Haar μ sur G. Il n'est pas trop difficile de montrer que la transformée de Fourier d'une fonction L1 sur G est une fonction continue bornée sur
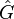
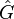
où l'intégrale est relative à la mesure de Haar ν sur le groupe dual
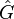
Théorèmes d'inversion de Plancherel et Fourier
Comme énoncé ci-dessus, le groupe dual d'un groupe abélien localement compact est lui aussi un groupe abélien localement compact et par suite possède une mesure de Haar ν, ou plus précisément une famille de mesures de Haar cν déterminées à un facteur multiplicatif positif près c.
Théorème: il existe un multiple positif de la mesure de Haar sur le groupe dual G^ de G telle que la restriction de la transformée de Fourier aux fonctions continues à support compact de G soit une isométrie linéaire. Elle s'étend de façon unique à un opérateur linéaire
où ν est la mesure de Haar sur le groupe dual.
Pour un groupe localement compact non compact, l'espace L1(G) ne contient pas L2(G), et il est nécessaire d'utiliser une astuce technique comme la restriction à un sous-espace dense.
En suivant Loomis (référence ci-dessous), on dit que les mesures de Haar sur G et G^ sont associées si la formule d'inversion de Fourier est satisfaite. Le caractère unitaire de la transformée de Fourier entraîne la formule de Plancherel :
pour toute fonction continue sur G à valeur complexe et support compact.
C'est cette extension unitaire de la transformée de Fourier que l'on considère comme étant la transformée de Fourier sur l'espace des fonctions de carré intégrable. Le groupe dual possède aussi sa transformée de Fourier inverse ; c'est l'inverse (ou adjoint, puisque nous sommes dans le cas unitaire) de la transformée de Fourier, comme cela est énoncé par le résultat suivant.
Théorème. L'adjoint de la transformée de Fourier restreinte au sous-espace des fonctions continues à support compact sur G est la transformée de Fourier inverse
où les mesures de Haar de G et G^sont associées.
Dans le cas où G = Rn, nous avons G^ = Rn et l'on retrouve la transformée de Fourier usuelle de Rn en prenant
Dans le cas où G est le groupe
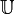

Si G est un groupe fini, F n'est autre que la transformée de Fourier discrète.
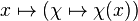
 = \int_G f(x - y) g(y)\, d \mu(y).](https://static.techno-science.net/illustration/Definitions/autres/0/032a5f2e091473015145589ecdf3ba91_303ce88f92c43f7baa4b5cc39daf8e8c.png)