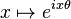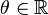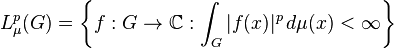Dualité de Pontryagin - Définition

Introduction

En mathématiques, notamment en analyse harmonique et dans la théorie des groupes topologiques, la dualité de Pontryagin explique les principales propriétés de la transformée de Fourier. Elle place dans un cadre plus général certaines observations à propos de fonction définies sur ou sur un groupe abélien fini:

• Les fonctions périodiques à valeur complexe suffisamment régulières ont une série de Fourier et on peut les déduire de cette série;
• Les fonctions à valeur complexe suffisamment régulières ont une transformée de Fourier et, tout comme les fonctions périodiques, on peut les déduire de cette transformée;
• Les fonctions à valeur complexe sur un groupe abélien fini ont une transformée de Fourier discrète définie sur le groupe dual, qui n'est pas canoniquement isomorphe au groupe de départ. De plus, toute fonction sur un groupe fini peut être déduite de sa transformée de Fourier discrète.

La théorie, introduite par Lev Semenovich Pontryagin et combinée avec la mesure de Haar introduite par John von Neumann, André Weil et d'autres, dépend de la théorie du d'un groupe abélien localement compact.

Mesure de Haar

Un groupe topologique G est localement compact si et seulement si l'élément neutre e du groupe admet un voisinage compact, ce qui équivaut encore à ce que e possède une base de voisinages compacts. Un des faits les plus remarquables à propos des groupes localement compacts est qu'ils peuvent être munis d'une mesure naturelle, unique à un facteur multiplicatif près : la mesure de Haar, qui permet de mesurer la « taille » d'un sous-ensemble suffisamment régulier de G. Ici, « suffisamment régulier » signifie être un borélien, c'est-à-dire un élément de la σ-algebre générée par les ensembles compacts. Plus précisément, une mesure de Haar à droite sur un groupe localement compact G est une mesure μ définie sur les boréliens de G, qui est invariante par translation à droite dans le sens où μ(Ax) = μ(A) si A est un borélien et x un élément de G.

La mesure de Haar nous permet de définir la notion d'intégrale pour une fonction mesurable à valeur complexe définie sur le groupe. En particulier, on peut considérer les espaces L^p associés à la mesure de Haar. Plus précisément :

Divers exemples de groupes abéliens localement compact sont donnés par :

• avec l'addition comme opération de groupe.
• Les réels strictement positifs munis de la multiplication. Ce groupe est clairement isomorphe à R, cet isomorphisme étant la fonction exponentielle.
• N'importe quel groupe abélien fini, muni de la topologie discrète. Par le théorème sur la structure de ces groupes, ce sont des produits de groupes cycliques.
• Le groupe des entiers muni aussi de la topologie discrète
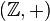
• Le cercle unité de (ie le groupe des complexes de module 1). est isomorphe en tant que groupe topologique au groupe quotient .
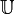
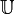
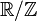
• Le corps des nombres p-adiques muni de l'addition, avec la topologie p-adique usuelle.

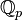
Exemples

Un caractère du groupe cyclique infini des entiers est déterminé par sa valeur en 1, générateur de . En effet pour tout caractère χ de , on a χ(n) = χ(1)ⁿ car χ est un morphisme de groupes, et cette formule montre que l'on définit de manière unique un caractère par sa valeur en 1. Ainsi le dual de est algébriquement isomorphe au cercle unité . La topologie de convergence sur les compacts est alors la topologie de la convergence simple. On montre aisément que c'est la topologie induite par le plan complexe.

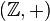
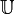
Le groupe dual de est donc canoniquement isomorphe à .

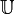
Réciproquement, un caractère de est de la forme , n entier. Comme est compact, la topologie sur le groupe dual est celle de la convergence uniforme, qui est ici la topologie discrète. Ainsi le dual de est canoniquement isomorphe à .

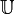
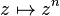
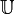
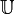
Le groupe des réels est isomorphe à son dual, les caractères de étant de la forme , . Avec ces dualités, la nouvelle version de la transformée de Fourier présentée ci-après coïncide avec la transformée de Fourier classique sur .