Échelle de temps en mécanique classique - Définition

Echelles de temps et mouvement keplerien

Néanmoins, en 2006, on a bien compris que le problème mécanique newtonien était "simplement" de résoudre des équations différentielles de la variable t , dit temps absolu. Et depuis 300 ans, les mathématiciens ne se sont pas privés de changer de variable pour résoudre ces équations, le plus aisément possible (cf mouvement keplerien):

méthode de Clairaut-Binet

Voici une échelle de temps particulièrement utile pour le mouvement avec Force centrale: il s'agit du changement choisi par Clairaut, puis enseigné par Binet à l'École Polytechnique : comme le champ est central, la deuxième loi de Kepler indique que, si r(t) non nul, l'angle polaire, θ(t), est fonction monotone croissante de t : on peut donc le choisir comme échelle de temps (cela serait le temps solaire vrai si l'inclinaison de la terre était nulle). Soit :

• en ayant posé u := 1/r
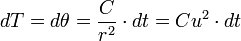
• un calcul mène à exprimer le vecteur vitesse :

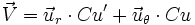
• de même le vecteur accélération :

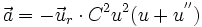
Cela convient "miraculeusement bien" pour la force newtonienne -GM m u², car on est conduit à une équation d'oscillateur harmonique :

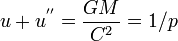
d'où la solution de Kepler u = 1/p + 1/p.e.cos(T-To).

Mais cette méthode ne convient pas si C = 0 (cas du choc).

Méthode de Levi-Civita

On préfère donc parfois choisir une échelle de temps dite régularisante , qui dans le cas de Newton , est appelée échelle de Levi-Civita (bien qu'elle fût connue depuis longtemps. On parle aussi d'échelle KS (Kustaanheimo et Stiefel)) : dT = dt/r, ce qui évite la divergence des intégrales quand r tend vers zéro.

En fait, pour simplifier, on s'intéresse au cas elliptique ; on prendra donc dT = sqrt(-2E)dt/r = Kdt/r (de telle sorte que ce temps T soit adimensionné) : reprenant alors les calculs du cas de changement d'échelle non-affine , on voit qu'il vient :

d OM /dT = v r/K ; puis .

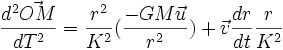
Or le vecteur de Runge-Lenz peut s'écrire :

 ;

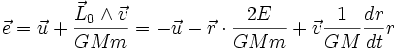
ce qui en remplaçant dans l'équation précédente donne :

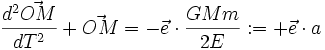
équation d'un oscillateur harmonique, de centre de force excentré !

Bien sûr , tout cela n'est, à ce niveau de sophistication, que poudre aux yeux, puisque l'on a reconnu en T la définition de l'anomalie excentrique et donc que : .

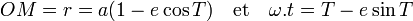
Mais dans une analyse de symétrie plus soigneuse, il est important de savoir faire ce changement d'échelle.