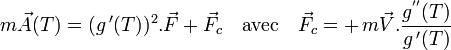Échelle de temps en mécanique classique - Définition

Introduction

En mécanique classique, le temps est ABSOLU : on l'appelle temps newtonien, t.

Pour résoudre certains problèmes théoriques de mécanique (c'est-à-dire résoudre certaines équations différentielles) , il est parfois astucieux de changer d' échelle de temps , c'est-à-dire , de choisir un nouveau paramètre T =f(t), où t → f(t) est une fonction croissante de t .

Changement affine

Dans l'équation du Principe Fondamental de la Dynamique , changer t en at+b , ne change que l'origine de la date et l'unité de temps ; ce qui est légitime.

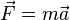
Méthode de Newton

Newton était bien conscient du fait que changer d'échelle de temps n'était pas anodin! On peut en poursuivant cette analyse retrouver la très célèbre transmutation de la force, de la force de Hooke en la force de gravitation, surtout en tenant compte des formules de l'accélération de Siacci.

Ainsi Newton montra que la MEME trajectoire pouvait être parcourue sous l'action de deux champs centraux différents, certes avec deux mouvements différents:

soit S le premier centre de force. Soit Q le deuxième centre de force, et QM le rayon vecteur. La tangente en M est la même pour les deux mouvements (mais V est différent de v, comme vu précédemment). Soit G le point de cette tangente, intersection avec la demi-droite SG menée de S parallèlement à QM.

Le théorème de Newton est :

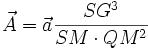
Passage de Hooke à Kepler

Dans le cas d'une ellipse de Hooke (de grand axe 2a), décrite sous l'action d'un champ central issu de O , centre de l'ellipse , et de force -k OM , le théorème précédent conclut : Cette même ellipse peut être décrite par le champ central issu de F avec :

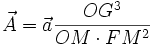
Or , géométriquement, il est facile de prouver que OG = a = cste:

D'où :

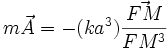
Newton en déduisit que l'ellipse de Kepler pouvait être décrite sous l'action d'une force centrale issue du foyer et en 1/ FM².

On voit ce que peut donner dans des mains expertes la notion de temps-non-absolu! En fait , si Newton a effectivement utilisé la formule précédente, il n'apparaît pas qu'il ait utilisé le changement d'échelle de temps : sa démonstration est directement un tour-de-force géométrique.

Changement non affine, force complémentaire

(Ce paragraphe exige de bien manier les dérivées).

Soit T = f(t) et soit t = g(T) la fonction réciproque.

Commencer par examiner ce que cela entraîne au niveau cinématique :

L'intervalle dT au temps t = t₀ vaudra .

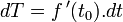
Donc si l'ancienne vitesse était , la nouvelle est . soit réduite du facteur d'échelle (égal d'ailleurs à , bien sûr):

.

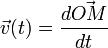
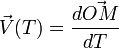
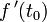
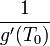
mais ce facteur d'échelle varie au cours du temps ! Donc, attention à la deuxième dérivation, c'est-à-dire pour l'accélération ! En effet :

Si d²f/dt²(t) = 0 , rien de grave n'arrive :

 : c'est le changement d'échelle sur l'accélération.

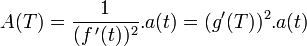
Sinon , c'est un peu plus compliqué : il ya "composition" des accélérations :

, relation involutive.

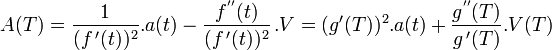
nota-bene : attention, f"(t) = d²f/dt² , g"(T) =d²g/dT², et si d(g')/(g') = -d(f')/(f') , on a bien g"/g' = - f"/f'^2 et f"/f' = -g"/g'^2 : la notation est trompeuse.

• Donc, avec un "faux-temps" (un temps non-absolu) , le PFDT se réécrit :

Il apparaît donc, en mécanique classique, dans un référentiel galiléen, une force complémentaire, F_c, due au fait que le temps utilisé n'est pas un temps absolu.

Ceci peut être utilisé à des fins astucieuses de résolution d'équations différentielles ; mais plus fondamentalement, on peut se poser la question de la "recherche du temps absolu", exactement de la même manière que se pose la question du référentiel absolu] ( entendre ici , galiléen). De même que la notion de Force de Coriolis apparaît grâce à l'analyse soignée de la notion de référentiel en rotation ( en sus de la force déjà bien décrite de force d'inertie d'entraînement), de même ici apparaît la force complémentaire de "non-utilisation" de temps absolu. Newton, qui indique explicitement au début des Principia que le temps est absolu, utilisera ce pseudo-temps, ce temps non-absolu, de façon remarquable.