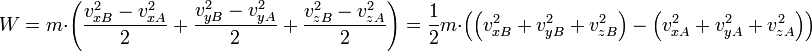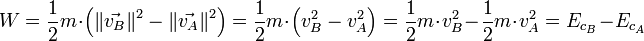Énergie cinétique - Définition
La liste des auteurs de cet article est disponible ici.
Théorème de König
L'expression (1) n'est guère utilisable directement, bien que générale. Il est possible de la réécrire sous une autre forme, dont l'interprétation physique est plus aisée.
Enoncé
Ce théorème se démontre en faisant intervenir le référentiel barycentrique (R*) lié au centre d'inertie G du système, et en mouvement de translation par rapport au référentiel d'étude (R). Il s'écrit:
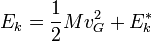
L'énergie cinétique d'un système est alors la somme de deux termes: l'énergie cinétique du centre de masse de (S) affectée de sa masse totale M,
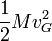
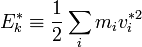
Application à un solide
Un solide est un système de points tels que les distances entre deux points quelconques de (S) sont constantes. Il s'agit d'une idéalisation d'un solide réel, considéré comme absolument rigide.
Cas général : axe instantané de rotation
Dans ce cas, le mouvement du solide peut être décomposé en un mouvement de son centre de masse G dans (R) et un mouvement de rotation autour d'un axe instantané (Δ) dans le référentiel barycentrique (R*).
Plus précisément, pour un solide on peut écrire le champ des vitesses dans le référentiel barycentrique (R*) sous la forme
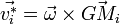
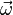
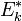
-
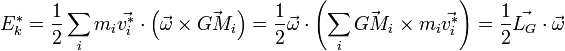
puisque
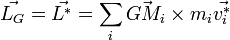
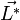
D'après le théorème de König, l’énergie cinétique totale d’un solide s'écrit donc ainsi:
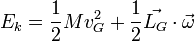
que l'on peut considérer comme la somme d’une énergie cinétique "de translation" et d’une énergie cinétique de rotation
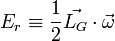
Cas de la rotation autour d'un axe fixe
Si, de surcroît, il y a rotation autour d'un axe (Δ) fixe dans (R), le moment cinétique par rapport à G du solide s'écrit
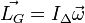
-
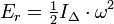
Unité
L'unité légale est le joule. Les calculs s'effectuent avec les masses en kg et les vitesses en
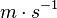
Théorème de l’énergie cinétique
Ce théorème, valable uniquement dans le cadre de la mécanique newtonienne, permet de lier l’énergie cinétique d’un système au travail des forces auxquelles celui-ci est soumis.
Énoncé
Dans un référentiel galiléen, pour un corps ponctuel de masse m constante parcourant un chemin reliant un point A à un point B, la variation d’énergie cinétique est égale à la somme W des travaux des forces extérieures et intérieures qui s’exercent sur le solide en question :
où EkA et EkB sont respectivement l’énergie cinétique du solide aux points A et B.
Démonstration
D’après la 2e loi de Newton, l’accélération du centre de gravité est liée aux forces qui s’exercent sur le solide par la relation suivante :
Pendant une durée dt, le solide se déplace de
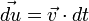

Si le solide parcourt un chemin d’un point A à un point B, alors le travail total s’obtient en faisant une intégrale le long du chemin :
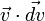
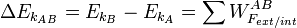
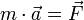
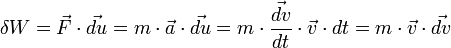
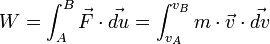
![W=m\cdot\int_{v_A}^{v_B}\vec{v}\cdot\vec{dv} = m\cdot\left (\int_{v_{xA}}^{v_{xB}}v_x\cdot dv_x+\int_{v_{yA}}^{v_{yB}}v_y\cdot dv_y+\int_{v_{zA}}^{v_{zB}}v_z\cdot dv_z\right )=m\cdot\left (\left[ \frac{v_x^2}{2} \right]_{v_{xA}}^{v_{xB}}+\left[ \frac{v_y^2}{2} \right]_{v_{yA}}^{v_{yB}}+\left[ \frac{v_z^2}{2} \right]_{v_{zA}}^{v_{zB}}\right )](https://static.techno-science.net/illustration/Definitions/autres/f/fc56f4a458cbcf16b949629b5facb79a_16e17da528faa1d5c01c53a3d4759210.png)