Énergie cinétique - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Historique - Définitions - Conventions - Théorème de König - Unité - Théorème de l’énergie cinétique - En mécanique relativiste - L’énergie thermique en tant qu’énergie cinétique - Théorème de la puissance cinétique

Introduction

Les véhicules des montagnes russes atteignent leur maximum d'énergie cinétique au bas de leur parcours. Lorsqu'ils commencent à monter, l'énergie cinétique commence à être transformée en énergie potentielle. La somme de l'énergie cinétique et potentielle du système reste constante, si on néglige les pertes (relativement faibles) dues aux frottements

L'énergie cinétique est l’énergie que possède un corps du fait de son mouvement réel. L’énergie cinétique d’un corps est égale au travail nécessaire pour faire passer le dit corps du repos à son mouvement de translation ou de rotation.

Historique

Gottfried Leibniz, s'opposant ainsi à Descartes, qui estimait que la quantité de mouvement se conservait toujours, développa l'idée de la « force vive » (vis viva), à laquelle il attribuait la valeur $m v 2$ . La force vive est donc le double de l'énergie cinétique.

« Il y a longtemps déjà que j’ai corrigé la doctrine de la conservation de la quantité de mouvement, et que j’ai posé à sa place quelque chose d’absolu, justement la chose qu’il faut, la force (vive) absolue… On peut prouver, par raison et par expérience, que c’est la force vive qui se conserve… »

Définitions

$E c$ formule approximative de l'énergie cinétique selon la masse et la vitesse utilisée lorsque la vitesse est faible devant la vitesse de la lumière:

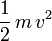
où m est la masse, et v la vitesse. Exemple : 1/2 x 45 kg x (8,3 m/s)² = 1550,025 joules

Cas d'un point matériel

Dans le domaine de validité de la mécanique newtonienne, la notion d'énergie cinétique peut être facilement mise en évidence pour un point matériel, corps considéré comme ponctuel de masse m constante.

En effet, la relation fondamentale de la dynamique s'écrit :

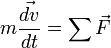
$m\frac{\vec{dv}}{dt}=\sum \vec{F}$ , avec $\sum \vec{F}$ somme des forces appliquées au point matériel de masse m (y compris les "forces d'inertie" dans le cas d'un référentiel non galiléen).

En prenant le produit scalaire, membre à membre, par la vitesse $\vec{v}$ du corps, il vient :

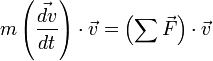
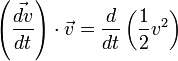
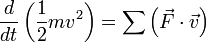
$m\left (\frac{\vec{dv}}{dt}\right )\cdot \vec{v}=\left (\sum \vec{F}\right ) \cdot \vec{v}$ , or $\left (\frac{\vec{dv}}{dt}\right )\cdot \vec{v}=\frac{d}{dt}\left ( \frac{1}{2}v^{2}\right )$ , il vient ainsi : $\frac{d}{dt}\left ( \frac{1}{2}mv^{2}\right )=\sum \left (\vec{F}\cdot \vec{v}\right )$ .

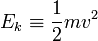
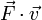
On met en évidence dans le membre de gauche la quantité $E_{k}\equiv \frac{1}{2}mv^{2}$ appelée énergie cinétique du point matériel, dont la variation est égale à la somme des puissances $\vec{F}\cdot \vec{v}$ des forces appliquées au corps (théorème de l'énergie cinétique, forme "instantanée").

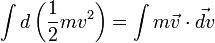
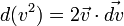
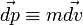
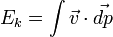
On peut obtenir une expression plus générale en considérant que l'on a donc $\int d\left (\frac{1}{2}mv^{2}\right )=\int m\vec{v}\cdot \vec{dv}$ , puisque $d(v^{2})=2\vec{v}\cdot \vec{dv}$ . En introduisant la variation infinitésimale de la quantité de mouvement du corps, $\vec{dp}\equiv m\vec{dv}$ , il vient au final l'expression : $E_k = \int \vec{v} \cdot \vec{dp}$ .

Cas d'un système de points

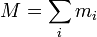
Dans le cas d'un corps que l'on ne peut considérer ponctuel, il est possible de l'assimiler à un système (d'une infinité) de points matériels $M i$ de masses $m i$ avec $M=\sum_{i} m_{i}\qquad$ masse totale du corps.

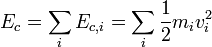
L'énergie cinétique $E c$ du système de points peut être alors simplement définie comme la somme des énergies cinétiques associées aux points matériels constituant le système : $E_{c}=\sum_{i} E_{c,i} = \sum_{i} \frac{1}{2}m_{i}v_{i}^{2}$ , (1). Cette expression est générale et ne préjuge pas de la nature du système, déformable ou pas.

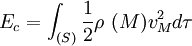
Remarque : en considérant la limite des milieux continus on a $E_{c}=\int_{(S)} \frac{1}{2}\rho\ (M)v_{M}^{2}d\tau\$ , M étant un point courant du système (S).

Conventions

L'énergie cinétique est généralement notée $E c$ ou $E k$ , l'indice c faisant référence au mot « cinétique » et l'indice k à son équivalent anglais, « kinetic ».

Théorème de König