Ensemble algébrique - Définition

Ensembles algébriques projectifs

La géométrie algébrique projective est un cadre plus confortable que la géométrie affine. La projectivité est une propriété analogue à la compacité topologique. Le théorème de Bezout n'est vrai que pour des variétés projectives.

Cadre. Dans cette partie Pⁿ(k) désigne l'espace projectif de dimension n sur k, c'est-à-dire l'ensemble , où R est la relation d'équivalence (relation de colinéarité) identifiant deux points x et y si et seulement si x et y sont sur la même droite vectorielle. L'espace projectif de dimension n s'identifie donc à l'ensemble des droites vectorielles d'un k-espace vectoriel de dimension n+1. La classe dans Pⁿ(k) d'un point est notée . Les x_i sont les coordonnées homogènes du point .

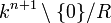
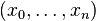
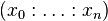
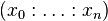
Définition. Soit S un ensemble de polynômes homogènes de l'anneau . On appelle ensemble algébrique (projectif) associé à S et on note Z ₊ (S) le sous-ensemble suivant de Pⁿ(k):

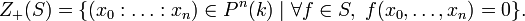
Remarquons que l'annulation du polynôme f en un point ne dépend que de la classe de celui-ci modulo la relation R. L'ensemble Z_+(S) est donc bien défini. L'indice + sert à distinguer les zéros homogènes des zéros affines.

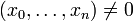
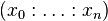
Exemple Soit F(X_0, X_1, X_2) un polynôme homogène à deux variables, non-nul, de degré d. L'ensemble algébrique projectif Z ₊ (F) du plan projectif P²(k) est appelé une courbe projective plane, de degré d. Le polynôme (où n un entier naturel) défini une courbe projective plane dont les points sont les solutions homogènes d'une équation de Pell-Fermat.

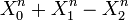
Remarque.

• Si I est l'idéal (homogène) de engendré par S, alors Z ₊ (I) = Z ₊ (S). Donc un ensemble algébrique projectif peut toujours être défini par un nombre fini de polynômes homogènes.

• Tout comme dans le cas des ensembles algébriques affines, il existe un théorème des zéros de Hilbert projectif qui établit une correspondance bijective entre les ensembles algébriques projectives dans Pⁿ(k) et les idéaux homogènes radiciels distincts de (idéal engendré par ). Un point de l'espace projectif correspond à un idéal premier homogène, maximal parmi ceux strictement contenus dans . À un point de coordonnées homogènes , on lui associe l'idéal engendré par les x_iX_j − x_jX_i, pour i et j variant entre 0 et n.

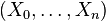
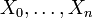
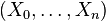
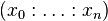
Propriétés:

1. Z ₊ ({0}) = Pⁿ(k), Z ₊ ({1}) est vide;
2. ;
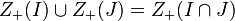
3. L'intersection d'une famille d'ensembles algébriques projectifs Z ₊ (I_λ) est égale à Z(I), où I est l'idéal engendré par .