Ensemble fini - Définition

Clôture sous les opérations usuelles

Une première remarque est que, comme tout sous-ensemble d'un ensemble fini est fini, on obtient directement la clôture par toute opération qui conduit à construire un sous-ensemble d'un des ensembles d'origine, comme l'intersection, ou la différence ensembliste.

Union

On va montrer que, comme attendu, la réunion de deux ensembles finis est finie, mais pour cela on envisage d'abord l’union disjointe (la réunion de deux ensembles disjoints, c'est-à-dire d'intersection vide), pour laquelle le cardinal correspond à l'addition :

Union disjointe

Si E et F sont deux ensembles finis disjoints, E de cardinal n et F de cardinal p alors E ∪ F, la réunion de ces deux ensembles, est finie. et de cardinal n + p.

Si E ∩ F = ∅, alors card(E ∪ F) = card E + card F.

On peut réaliser l'union disjointe de deux ensembles qui ne le sont pas en « colorant » leurs éléments, de façon distincte suivant qu'ils appartiennent à l'un ou à l'autre ensemble. Ainsi N_n × {0} et N_p × {1} sont deux ensembles disjoints, le premier étant en bijection avec N_n et le second avec N_p par oubli de la seconde composante. Par composition des bijections en jeu, il suffit de montrer le résultat précédent pour ces deux ensembles, à savoir que N_n × {0} ∪ N_p × {1} a pour cardinal n + p. On vérifie que l'application de cette réunion dans N_{n + p} et qui associe au couple (x, y) l'entier x + y n est une bijection.

Différence et intersection

Si E est un ensemble fini, et F un ensemble quelconque, E ∩ F, l'intersection de E et de F, ainsi que E − F leur différence, sont des sous-ensembles de E donc finis. Comme E est la réunion disjointe de ces deux ensembles, on en déduit que :

card E = card (E ∩ F) + card (E − F)

Union binaire

L'union de deux ensembles finis E et F peut se ramener à une réunion disjointe d'ensembles dont nous avons vu qu'ils étaient finis. En effet

E ∪ F = (E − F) ∪ (E ∩ F) ∪ (F − E).

On en déduit donc que si E et F sont deux ensembles finis, leur réunion est finie. De plus :

card(E ∪ F) = card E + card F - card(E ∩ F).

Union finie

On en déduit par récurrence qu'une réunion finie d'ensembles finis est finie. La formule obtenue pour le cardinal de la réunion se généralise.

.

Produit cartésien

Si E et F sont finis, de cardinaux respectifs n et p, E × F est fini de cardinal np.

Tout comme pour l'union disjointe, il suffit de montrer le résultat pour les ensembles d'entiers N_n et N_p. On montre que l'application qui au couple (x, y) associe (x+1)(y+1) - 1 établit une bijection de N_n × N_p dans N_np (il aurait été plus naturel d'établir une bijection de {1, …, n} × {1, …, p} dans {1, …, np} en associant xy à (x, y)).

Ensemble des parties

L'ensemble des parties P(E) d'un ensemble fini E de cardinal n est un ensemble fini de cardinal 2ⁿ.

De façon analogue aux cas précédents on peut se ramener à E = N_n, puisque si f est une bijection d'un ensemble A dans un ensemble B, elle induit une bijection de P(A) dans P(B), en associant à un sous-ensemble X de A le sous-ensemble de B des images par f des éléments de X.

On donne deux démonstrations de ce résultat, la première présuppose un peu plus de connaissances arithmétiques. À un ensemble X de N_n on associe par f l'entier dont la représentation binaire aura 1 comme i-ème chiffre quand i appartient à X, 0 sinon :

.

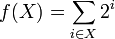
La valeur maximale atteinte par f l'est pour E (tous les chiffres de la représentation à 1) et f(E)=2ⁿ - 1. Un entier strictement inférieur à 2ⁿ à une représentation binaire de longueur inférieure à n. L'écriture binaire d'un entier est unique. On en déduit que La fonction f établit donc une bijection de P(E) dans N_2ⁿ.

On peut aussi se servir uniquement de la définition par récurrence de la fonction exponentielle :sur les entiers naturels. La fonction qui à un entier naturel n associe l'entier naturel 2ⁿ est l'unique fonction de N dans N qui satisfait les équations :

2⁰=1 ;  2ⁿ⁺¹=2•2ⁿ

Il suffit donc de montrer que la fonction qui à un ensemble E de cardinal n associe le cardinal de son ensemble des parties P(E) satisfait ces équations.

C'est vrai pour l'ensemble vide, seul ensemble de cardinal 0, dont l'ensemble des parties est le singleton {∅} ayant pour seul élément cet ensemble.

Soit E un ensemble de cardinal n +1, et qui a donc au moins un élément soit e. Un sous-ensemble de E a ou n'a pas e pour élément. Ceci permet de partager en deux l'ensemble des parties de E :

.

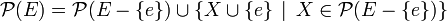
Ces deux ensembles sont disjoints et de même cardinal, par la bijection qui consiste à ajouter e, d'où le résultat. On a bien montré que, si e n'appartient pas à A de cardinal fini :

et donc si E est un ensemble fini :

.

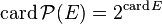
Ensemble des applications d'un ensemble fini dans un ensemble fini

L'ensemble des applications d'un ensemble fini de cardinal n dans un ensemble fini de cardinal p, est un ensemble fini de cardinal pⁿ.

Il y a une bijection évidente de l'ensemble des parties d'un ensemble E dans l'ensemble des applications de E dans {0,1} en associant à un sous-ensemble de E sa fonction caractéristique. C'est le cas particulier p = 2. Le cas général se traite de façon analogue à ce qui a été fait pour l'ensemble des parties.