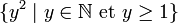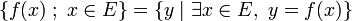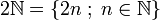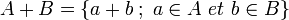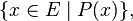Ensemble - Définition
La liste des auteurs de cet article est disponible ici.
Ensemble défini comme image directe
Pour noter l'ensemble des carrés parfaits non nuls (voir exemple au paragraphe précédent) on peut utiliser la notation plus concise :
dont la forme générale est :
Elle représente l'ensemble des images d'un ensemble E par une application f. L'ensemble obtenu s'appelle image directe de E par f. Il s'agit d'une variante de la notation en compréhension ci-dessus. Elle se déduit de celle-ci, en utilisant la définition d'une fonction, si F est l'ensemble d'arrivée de la fonction f :
-
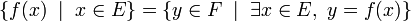
De cette notation dérivent d'autres notations facile à comprendre
Ces notations ont leur avantage et leur inconvénient. D'un côté, elles facilitent une compréhension immédiate des ensembles considérés et rendent accessibles à l'intuition des objets plus compliqués. D'un autre côté, ces notations masquent un quantificateur existentiel indispensable dès lors que l'on veut utiliser cet ensemble.
Définition d’un ensemble en compréhension
Un ensemble peut être défini en compréhension, c’est-à-dire qu'on le définit par une propriété caractéristique parmi les éléments d'un ensemble donné. Ainsi l'ensemble des entiers naturels pairs est clairement défini par compréhension, par la propriété « être pair » parmi les entiers naturels. On peut utiliser la notation d'un ensemble en compréhension, par exemple pour l'ensemble des entiers naturels pairs, on écrira (

-
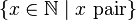
On définira de la même façon (
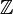
-
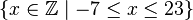
-
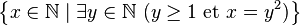
La formulation générale est :
Cette construction a besoin d'un ensemble déjà existant E et d'une propriété P définie sur tous les éléments de E. Elle permet donc de construire des sous-ensembles mais pas la réunion d'une famille d'ensembles, ni l'ensemble des parties d'un ensemble, ni même les ensembles finis définis par la liste de leurs éléments comme au paragraphe précédent. On pourrait pourtant écrire, par exemple pour l'ensemble des parties P(E) = { A | A ⊂ E }
Il n'est pas pour autant pour autant possible de définir un ensemble par n'importe quelle propriété, et lever entièrement la restriction de la compréhension. Si c'était le cas on pourrait définir l'ensemble {x | x ∉ x}, ce qui conduit à une contradiction (c'est le paradoxe de Russell). La restriction de la compréhension à un ensemble connu protège contre ce genre de paradoxes, elle correspond directement au schéma d'axiomes de compréhension de la théorie de Zermelo. Cette restriction ne peut se lever que dans des cas particuliers précis, qui correspondent à d'autres axiomes de la théorie de Zermelo (axiome de la paire, axiome de la réunion, axiome de l'ensemble des parties).
On n'a pas dit ce que l'on entendait par « propriété » ou « condition ». Malgré la restriction précédente, on ne peut tout autoriser, sous peine d'autres paradoxes comme le paradoxe de Richard ou le paradoxe de Berry, qui fait intervenir, par exemple, « l'ensemble des entiers naturels définissables en moins de quinze mots français ». Il est nécessaire de préciser le langage dans lequel on peut définir ces conditions. En particulier ce langage doit être défini a priori, et ne peut être étendu qu'à l'aide de définitions qui sont soit de simples abréviations, soit résultent de preuves d'existence et d'unicité.