Axiome de la réunion - Définition
Dans la théorie axiomatique des ensembles et dans les branches de la logique, des mathématiques, et de l'informatique, l'axiome de la réunion est l'un des axiomes de la théorie des ensembles de Zermelo-Fraenkel, affirmant que, pour tout ensemble quelconque, il existe un ensemble qui contient exactement les éléments de tout élément de l'ensemble.
Cet axiome, permet avec l'aide de l'axiome de la paire de démontrer que la réunion de deux ensembles (qui contient exactement les éléments des deux ensembles), est un ensemble.
Dans le langage formel de l'axiomatique de Zermelo-Fraenkel, l'axiome s'écrit:
![\forall A\ \exists B\ \forall C\ [ C\in B\Leftrightarrow \exists D\ (D\in A\wedge C\in D) ]](https://static.techno-science.net/illustration/Definitions/autres/1/19004ea251dee647754c8a031602cbc7_4e220d4d9b88643b51b35d1ac8307eb9.png)
ou avec des mots:
- étant donné un ensemble quelconque A, il existe un ensemble B tel que, pour tout ensemble C quelconque, C est élément de B si et seulement s’il existe un ensemble D tel que D soit un élément A et que C soit un élément de D.
Pour comprendre cet axiome, notez que la clause placée entre parenthèses et faisant intervenir D dans l'affirmation symbolique ci-dessus, sert à déclarer que C est élément d'un certain ensemble lui-même élément de A. Ainsi, l'axiome affirme réellement qu'étant donné un ensemble A, nous pouvons trouver un ensemble B dont les éléments sont précisément les éléments des éléments de A. Nous pouvons employer l'axiome d'extensionnalité pour prouver que cet ensemble B est unique. Nous appelons l'ensemble B la réunion de A, et le notons
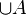
- la réunion d'un ensemble, dit de façon plus commune la réunion de tous les éléments de cet ensemble, est un ensemble
L'axiome de la réunion ou un équivalent de celui-ci apparaît dans pratiquement toute axiomatique alternative de la théorie des ensembles.
Notez qu'il n'y a aucun axiome correspondant pour l'intersection. Dans le cas où A est l'ensemble vide, il n'y a aucune intersection de A dans la théorie des ensembles de Zermelo-Fraenkel. D'autre part, si A a un certain élément B, nous pouvons former l'ensemble