Entier algébrique - Définition

Exemples

Entiers relatifs

L'anneau Z est un anneau d'entiers au sens des définitions précédentes :

• L'anneau Z est la fermeture intégrale de Z dans Q.

Ainsi la définition de l'intégralité s'applique aussi à Z. Sur tout corps de nombres les éléments de Z sont entiers, cette définition généralise bien la définition d'un entier.

On remarque que tout élément de Z est entier sur Z.

Réciproquement, soit α un nombre rationnel entier sur Z. Il s'écrit sous la forme α = a / b avec a et b deux entiers tels que b soit strictement positif, a et b soient premiers entre eux. Soit

un polynôme qui annule α. L'égalité suivante est vérifiée :

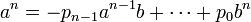
Soit π un nombre premier divisant b, il divise le terme de droite de l'égalité ci-dessus. On en déduit qu'il divise aⁿ et donc a. Or a et b sont premiers entre eux, par conséquent le seul diviseur de b est 1 et b est égal à 1. Par suite α est un entier relatif.

Cet énoncé ainsi que sa preuve se transpose dans tout anneau factoriel qui est donc intégralement clos.

Entier de Gauss

Les entiers de Gauss sont les nombres de la forme a + i.b avec a et b entiers relatifs. Ils sont éléments du corps des rationnels de Gauss, constitué des complexes de la forme α + i.β où α et β sont des nombres rationnels.

• Les entiers de Gauss forment la fermeture intégrale de Z dans le corps des rationnels de Gauss.

Les entiers de Gauss forment manifestement un anneau commutatif unitaire intègre, ils disposent d'une propriété supplémentaire :

• Les entiers de Gauss forment un anneau euclidien.

On trouve leur usage pour la résolution de certaines équations diophantiennes comme celle du théorème des deux carrés de Fermat.

Remarque : Les démonstrations se trouvent dans l'article détaillé.

Entier quadratique

Les entiers de Gauss représentent un cas particulier d'une famille plus générale d'anneaux. Ils correspondent aux fermetures intégrales de Z dans les plus petit corps contenant les racines d'un polynôme irréductible du deuxième degré à coefficients dans Q. De tels corps sont appelés corps quadratiques.

• Soit K un corps quadratique, il existe un entier d sans facteur carré tel que K est égal à Q[√d].

Ici, d peut être négatif, dans ce cas √d désigne la classe de X dans l'anneau quotient Q[X] / (X²- d) isomorphe au plus petit sous-corps de C contenant i √|d|. Cette propriété est démontrée dans l'article Extension quadratique.

• La fermeture intégrale O_Q[√d] de Z dans le corps quadratique Q[√d] est le plus petit anneau unitaire contenant u où u est défini par :

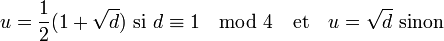
• L'ensemble O_Q[√d] est un sous-anneau de C.

Certains anneaux Z[√d] ne sont pas intégralement clos. Ainsi Z[√-3] n'est pas la fermeture intégrale de Z dans Q[√-3] (qui est égale à Z[j] si j désigne la racine cubique de l'unité à composante imaginaire strictement positive). L'anneau Z[j] composé d'éléments appelés entiers d'Eisenstein est euclidien, en revanche Z[√-3] n'est ni euclidien ni principal ni même factoriel. En effet, dans cet anneau l'entier 4 admet deux décompositions en facteurs irréductibles :

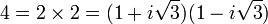
Remarque : Les deux dernières propositions sont démontrées dans l'article associé.