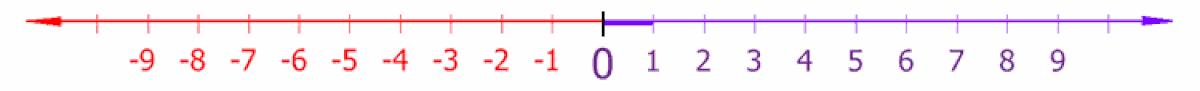Entier relatif - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Motivation - Règles opératoires - Fragments d'histoire - Ensemble des entiers

Introduction

En mathématiques, un entier relatif se présente comme un entier naturel muni d'un signe positif ou négatif qui indique sa position par rapport à zéro sur un axe orienté. Les entiers positifs (supérieurs à zéro) s'identifient aux entiers naturels : 0, 1, 2, 3… tandis que les entiers négatifs sont leur opposés : 0, −1, −2, −3… L'entier zéro lui-même est donc le seul nombre à la fois positif et négatif.

Un nombre réel est entier s'il est sans partie fractionnaire, c'est-à-dire si son écriture décimale ne comprend pas de chiffre (autre que zéro) « après la virgule ».

Les entiers relatifs permettent d'exprimer un bilan de variation d'unités (positif pour un gain, négatif pour une perte) ou une position sur un axe orienté discret, par rapport à un point origine. Ils donnent un sens à la différence de deux entiers naturels quelconques.

L'ensemble des entiers relatifs est noté « Z », lettre capitale grasse dans les textes dactylographiés, peu à peu supplantée par la graphie manuscrite avec une double barre oblique : « $\mathbb{Z}$ ». La présence d'un astérisque en exposant (« Z* ») désigne en général l'ensemble des entiers relatifs non nuls, même si cette notation est utilisée parfois pour l'ensemble des éléments inversibles, c'est-à-dire la paire d'entiers {−1; 1}. La notation « Z⁻ » désigne l'ensemble des entiers négatifs. Il est plus rare de trouver la notation « Z⁺ », remplacée par la notation « N » des entiers naturels par identification.

Cet ensemble est (totalement) ordonné pour la relation de comparaison usuelle héritée des entiers naturels. Il est aussi muni des opérations d'addition et de multiplication qui fondent la notion d'anneau en algèbre.

Les entiers relatifs sont parfois appelés entiers rationnels, suivant la dénomination rational integer en anglais, et comme cas particuliers d'entiers algébriques sur le corps de nombres des rationnels. On trouve cette appellation chez Nicolas Bourbakiet certains mathématiciens s'inscrivant dans le mouvement des mathématiques modernes, parmi lesquels Georges Papy.

La droite des nombres permet de représenter les entiers relatifs

Motivation

La principale raison de l'introduction des nombres négatifs est la possibilité de résoudre toutes les équations de la forme :

a + x = b, où x est l'inconnue et a et b sont des paramètres.

Dans l'ensemble des entiers naturels, seules certaines de ces équations ont une solution.

5 + x = 8 si et seulement si x = 3

9 + x = 4 n'a pas de solution dans l'ensemble des entiers naturels. Elle possède une solution dans l'ensemble des entiers relatifs qui est -5.

Règles opératoires

Dans un nombre relatif, on distingue son signe (+ ou - ) et sa valeur absolue : - 3 a pour valeur absolue 3.

Addition

La somme de deux entiers de même signe s'obtient en additionnant les deux valeurs absolues et en conservant le signe commun

(-3) + (-5) = -8 écriture que l'on abrège en -3 - 5 = - 8 supprimant le signe opératoire +

La somme de deux entiers relatifs de signe contraire s'obtient en calculant la différence entre les deux valeurs absolue et en lui affectant le signe de l'entier ayant la plus grande valeur absolue

(+3) + (-5) = - 2 écriture que l'on abrège en 3 - 5 = - 2

Multiplication

Le résultat d'une multiplication s'appelle un produit. Le produit de deux nombres relatifs de même signe est toujours positif (+) et s'obtient en effectuant le produit des valeurs absolues: