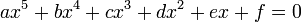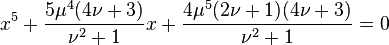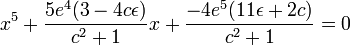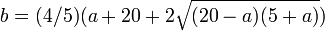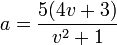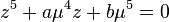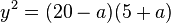Équation quintique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, une équation quintique est une équation polynôme dans laquelle le plus grand exposant de l'inconnue est 5. Elle est de forme générale :
où a, b, c, d, e, et f appartiennent à un corps (habituellement les nombres rationnels, les nombres réels ou les nombres complexes), et
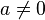
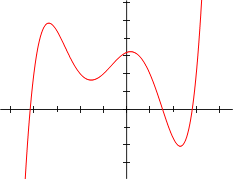
La fonction
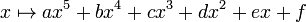
Trouver les racines d'une équation quintique
Trouver les racines d'un polynôme - valeurs de x qui satisfont une équation polynomiale - dans le cas des coefficients rationnels donnés a été un problème essentiel en mathématiques.
Résoudre les équations linéaires, quadratiques, cubique et quartique en factorisant par radicaux est relativement direct lorsque les racines sont rationnelles et réelles ; il existe aussi des formules qui fournissent les solutions cherchées. Par contre, il n'existe pas de formule pour les équations quintiques générales sur les rationnels en termes de radicaux ; ceci fut d'abord démontré par le théorème d'Abel-Ruffini découvert par Paolo Ruffini et Niels Henrik Abel. Publié en 1824, ce fut une des premières applications de la théorie des groupes en algèbre. Ce résultat est aussi valable pour les équations de degrés plus élevés. Cela est assez surprenant ; même s'il y a des racines, il n'y a pas d'expression algébrique finie de
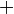

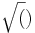
Certaines équations de degré cinq peuvent être résolues par factorisation en radicaux, par exemple :
-
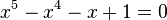
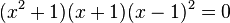
D'autres quintiques comme
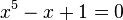
Évariste Galois développa des techniques pour déterminer si une équation donnée peut être résolue par radicaux, mais ceci touche au domaine de la théorie de Galois. En utilisant la théorie de Galois, John Stuart Glashan, George Paxton Young et Carl Runge montrèrent en 1885 que toute quintique irréductible résoluble dans la forme de Bring-Jerrard,
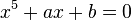
doit avoir la forme suivante :
où
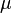
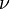
avec
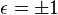
où
et en utilisant le cas négatif de la racine carrée, cela fournit, après ajustement des variables, la première paramétrisation tandis que le cas positif donne la seconde avec
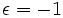
avec des coefficients rationnels doit satisfaire la simple courbe quadratique
pour certain rationnels a,y.
Il existe aussi d'autre méthodes de résolution de quintiques. Aux environs de 1835, Jerrard montra que les quintiques peuvent être résolues en utilisant les ultraradicaux (aussi connus sous le nom radicaux de Bring), les racines réelles de
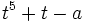
Les méthodes numériques telles que la méthode de Newton-Raphson avec des essais et des erreurs donnent des résultats très rapidement si seules les valeurs numériques pour les racines sont cherchées, ou s'il est connu que les solutions comprennent seulement des expressions simples (telles que celles des examens). D'autres méthodes telles que la méthode de Laguerre ou la méthode de Jenkins-Traub peuvent aussi être utilisées pour trouver numériquement de manière sûre les racines d'équations quintiques.