Espace d'interpolation - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En analyse, un espace d'interpolation ou espace interpolé est un espace qui se trouve entre deux autres espaces. Les applications les plus importantes de cette notion ont lieu pour les espaces de Sobolev de fonctions qui sont dérivables un nombre non entier de fois. Ces espaces sont créés par interpolation à partir des espaces de Sobolev de fonctions dérivables un nombre entier de fois.
Historique
La théorie de l'interpolation des espaces vectoriels a débuté par une observation faite par Józef Marcinkiewicz, et qui fut généralisée ultérieurement et connue sous le non de Théorème de Riesz-Thorin. En termes simples, si une fonction linéaire est continue sur un certain espace Lp et aussi sur un autre espace Lq, alors elle est aussi continue sur l'espace Lr, pour tout r compris entre p et q. En d'autres mots, Lr est un espace intermédiaire entre Lp et Lq.
Au cours du développement des espaces de Sobolev, il est devenu évident que les espaces des traces des fonctions des espaces de Sobolev n'étaient en aucune manière des espaces de Sobolev usuels (composés de fonctions différentiables un nombre entier de fois), et Jacques-Louis Lions a découvert que, de fait, ces espaces de traces étaient constitués de fonctions ayant un degré de différentiabilité non-entier.
De nombreuses méthodes ont été mises au point pour construire de tels espaces de fonctions : transformation de Fourier, interpolation complexe, interpolation réelle, dérivées fractionnaires,théorème de Chaatit, etc ...
Discussion technique
Dans cet article nous sommes intéressés par la situation suivante : X et Z sont des espaces de Banach, et X est un sous-ensemble de Z, mais la norme de X n'est pas la même que celle de Z. X est dit plongé continuement dans Z s'il existe une constante
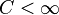
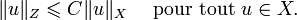
C'est le cas par exemple si X=
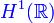
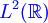
Soient X et Y deux espaces de Banach qui sont deux sous-ensembles de Z. De plus on définit des normes sur
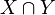
Alors les inclusions suivantes sont toutes continues :
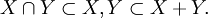
A partir de maintenant, l'espace Z ne joue plus aucun rôle, il a juste servi pour donner un sens à X+Y. Notre but maintenant est de construire des espaces intermédiaires entre X and Y dans le sens suivant :
- Définition : X et Y étant définis comme ci-dessus, un espace d'interpolation est un espace de Banach W ayant les propriétés suivantes :
Si L est opérateur linéaire de X+Y dans lui-même, qui est continu de X dans lui-même et de Y dans lui-même, alors L est aussi continu de W dans lui-même.
- De plus, l'espace W est dit d'exposant θ ( 0<θ<1 ) s'il existe une constante C telle que, quel que soit l'opérateur L satisfaisant les conditions ci-dessus, on ait :
-
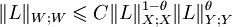
On a utilisé la notation
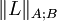
Il y a de nombreuses manières de construire des espaces interpolés ( et le théorème de Riesz-Thorin en est un exemple pour les espaces Lp). La méthode d'interpolation complexe est valable pour des espaces de Banach arbitraires.
Interpolation complexe
Si le champ des scalaires est celui des nombres complexes, alors on peut utiliser les propriétés des fonctions analytiques complexes pour définir un espace d'interpolation.
- Définition: Soient deux espaces de Banach X et Y, la méthode d'interpolation complexe consiste à considérer l'espace des fonctions analytiques f à valeurs dans X+Y, définie sur la bande ouverte
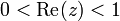
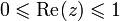
- f(iy) est borné dans X, f(1+iy) est borné dans Y.
- On définit la norme
- Et pour 0 < θ < 1, on définit
Il est alors facile de montrer que nous avons le
- Théorème: W = [X, Y]θ est un espace exactement interpolé d'exposant θ.
Interpolation réelle (par la méthode K)
La méthode K d'interpolation réelle peut être utilisée même quand le champ des scalaires est celui des nombres réels.
- Définition: Pour tout
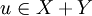
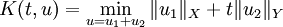
-
- Alors la méthode K d'interpolation réelle consiste à définir Kθ,q(X,Y) comme l'ensemble de tout les éléments u de X+Y tels que
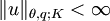
Kθ,q(X,Y) est un espace exactement interpolé de degré θ.
Interpolation réelle (par la méthode J)
Comme avec la méthode K, la méthode J peut aussi être utilisée pour les espaces vectoriels sur le corps des réels.
- Définition: Pour tout
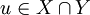
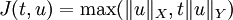
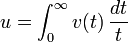
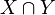
-
- La norme de u est
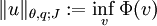
Ici encore, Jθ,q(X,Y) est un espace exactement interpolé de degré θ.
Relations entre les méthodes d'interpolation
Les deux méthodes d'interpolation réelles sont souvent équivalentes.
- Théorème: Si 0<θ<1 et 1 ≤ q ≤ ∞, alors Jθ,q(X,Y) = Kθ,q(X,Y) avec équivalence des normes.
Quand les deux méthodes sont équivalentes, on écrit [X,Y]θ,q pour la méthode d'interpolation réelle. En contraste, la méthode d'interpolation complexe n'est habituellement pas équivalente à la méthode d'interpolation réelle. Cependant, il y a quand même une relation entre les deux.
- Théorème: Si 0 < θ < 1, alors
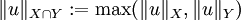
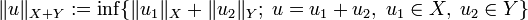
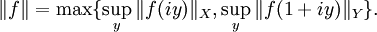
![[X,Y]_\theta = \{ u \in X+Y \}, \quad \text{ muni de la norme } \|u\| = \inf_{f(\theta)=u}\|f\|.](https://static.techno-science.net/illustration/Definitions/autres/4/40728a5585b913fa8c850644ee1cd3c4_a9e45a7ba5ea76a4675a8ea380056e54.png)
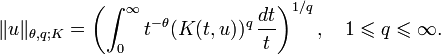
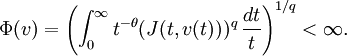
![[X,Y]_{\theta,1} \subset [X,Y]_\theta \subset [X,Y]_{\theta,\infty}.\,](https://static.techno-science.net/illustration/Definitions/autres/0/04b9ae50f79358efc9e44bb19938c34d_bce10e40bdd12187e2d98ab291649d57.png)

















































