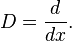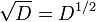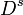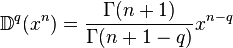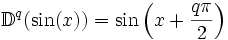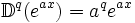Dérivées fractionnaires - Définition

Les Dérivées fractionnaires sont des outils mathématiques. Elles font partie des analyses mathématiques élaborés à partir de la transformation de Fourier (lorsque l'opérateur agit sur une variable d'espace), ou la transformation de Laplace (lorsque l'opérateur agit sur la variable de temps).

On peut définir par le même procédé des intégrations fractionnaires. Ces dérivées ou intégrations fractionnaires rentrent dans le cadre plus général des opérateurs pseudo-différentiels.

Ces dérivées fractionnaires sont utilisées par exemple dans certains domaines de la physique faisant intervenir des phénomènes de diffusion comme l'électromagnétisme, l'acoustique ou la thermique, en définissant des opérateurs pseudo-différentiels diffusifs, avec conditions de bord à "géométrie fractale".

Début de traduction de l'article anglais :

En mathématiques, l' analyse fractionnaire est une branche de l'analyse mathématique qui étudie la possibilité qu'un opérateur différentiel puisse être élevé à une puissance réelle.

Ceci vaut aussi pour un opérateur d'intégration J. ()

Dans ce contexte, puissances fait référence à une application itérative, dans le même sens que pour

f ²(x) = f(f(x)).

Par exemple, on peut se demander comment interpréter convenablement

comme la racine carrée de l' opérateur de dérivation (un opérateur à moitié itéré), c'est-à-dire une expression d'un certain opérateur qui, lorsquelle est appliquée deux fois à une fonction aura le même effet que la dérivation. Plus généralement, on peut examiner le problème de définir

pour des valeurs réelles de s, de telle sorte que lorsque s prend une valeur entière n, on récupère la dérivation n-ième usuelle pour n > 0, [...].

...

On peut ainsi arriver à quelques formules de base, permettant d'évaluer des dérivées "fractionnaires" dans quelques cas simples :

Ces formules sont issues de l'article en anglais sur les differintegrales de Riemann-Liouville