Fonction linéaire - Définition

Dans les mathématiques élémentaires, les fonctions linéaires sont les fonctions les plus simples que l'on rencontre. Ce sont des cas particuliers d'applications linéaires.

Elles traduisent la proportionnalité.

Par exemple, on dira que le prix d'un plein d'essence est fonction linéaire du nombre de litres mis dans le réservoir car :

• pour un litre, on paie 1,10 euros
• pour 2 litres on paie 2,20 euros
• pour 10 litres on paie 11 euros
• pour 100 litres on paie 110 euros

et pour x litres on paie 1,1 x euros.

Reconnaître une fonction linéaire

Une fonction linéaire est définie de la manière suivante :

avec y = a × x

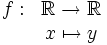
où le nombre a est un réel quelconque. Ce réel a s'appelle le coefficient de proportionnalité.

En repartant de l'égalité , on voit que, pour x différent de 0, on peut diviser les deux côtés par x. Il vient donc

.

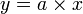
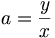
Il suffit donc d'une valeur x non nulle et de son image y pour déterminer la valeur du coefficient de proportionnalité.

Représentation dans le plan

La représentation graphique d'une fonction est l'ensemble des points de coordonnées (x ; y) tels que y = f(x).

Les fonctions linéaires définies de dans se représentent dans le plan par une droite. Cette droite passe par l'origine du repère. En effet, si M est un point de la représentation graphique tel que x = 0, il vient nécessairement y = 0.

L'élément graphique important est le coefficient directeur (ou pente) de la droite. Il correspond au coefficient de proportionnalité de la fonction linéaire. On retrouve alors un moyen simple de calcul de ce coefficient directeur : si M (x ; y) est un point de la droite différent de l'origine, nous avons, comme précédemment , puis par division par x (non nul)

.

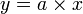
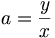
Il existe un moyen de lire sur le graphique la pente de la droite : c'est l'inclinaison de la droite par rapport à l'axe des abscisses.

Par exemple :

• si a = 1, la droite fait un angle de 45° avec l'axe des abscisses ;
• si a = 2, la droite monte plus fortement que pour a = 1 ;
• si a = 0, la droite est confondue avec l'axe des abscisses ;
• si a = -1, la droite descend.

Dans un quadrillage à l'unité, le coefficient directeur correspond au nombre de carreaux parcourus sur l'axe des ordonnées lorsqu'on se déplace d'un seul carreau sur celui des abscisses.