Flambage - Définition

Poteaux en béton armé

La formule d'Euler n'est pas applicable aux poteaux et butons en béton armé, en raison de la fissuration du béton l'inertie varie sur la longueur ce qui conduit à des calculs complexes. Un des pionniers de ce domaine de calculs fut Pierre Faessel qui établit des abaques de calculs.

Calcul pratique pour des matériaux homogènes

Ce problème est sérieusement considéré dans les cas du dimensionnement de poteaux ou de piliers et de bielles en mécanique, éléments nécessairement de grande longueur et soumis à la compression.

En pratique cependant, la formule d'Euler n'est pas directement utilisée pour dimensionner une poutre. Elle intervient toutefois sous une autre forme car optimiser le dimensionnement d'un poteau c'est choisir une section pour laquelle la résistance à la compression (liée à la limite élastique) sera sensiblement égale à la résistance au flambement (charge critique).

On définit habituellement un paramètre géométrique, λ, appelé coefficient d'élancement :

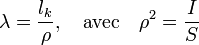
où ρ est le rayon de giration de la poutre et S la section de cette poutre.

On peut alors définir un coefficient d'élancement critique, λ_c, qui ne dépend que des propriétés du matériau :

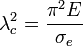
où σ_e est la limite élastique du matériau ;

On peut alors déterminer la charge critique F_c applicable sur une poutre en comparant sa valeur d'élancement λ à la valeur de λ_c.

• Si , la poutre est en compression simple :
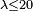
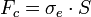
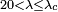
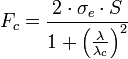
• Si , on utilise alors la formule expérimentale de Rankine :
• Si , on utilise alors la formule d'Euler, qui peut se réecrire sous la forme :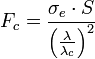

Ces considérations ne tiennent pas compte des imperfections inhérentes à la production des barres ; celles-ci ont pour conséquence de mener à un flambage précoce de la barre, sous-estimé par la formule d'Euler. Dans la pratique, on introduit un facteur de flambage χ servant à réduire la résistance en section de la barre (compression simple)

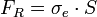
pour arriver à sa résistance globale en compression

.

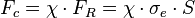
Ce facteur de flambage, issu de résultats expérimentaux, est généralement défini comme suit :

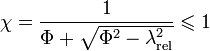
où λ_rel est le coefficient d'élancement relatif (sans dimension)

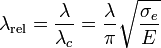
et Φ est un facteur défini selon le matériau utilisé et le type d'imperfections. À titre d'exemple, dans la norme suisse pour l'acier ce facteur s'écrit :

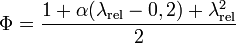
Dans cette formule, α est le facteur d'imperfection du matériau ; il dépend de la direction de flambage considérée et du procédé de fabrication.

Géologie

En géologie, on trouve aussi le phénomène de flambage, mais à une échelle bien plus grande qu'en RDM. La compression d'une masse continentale importante provoque à l'échelle locale ou régionale la formation d'une chaine de montagne. À l'échelle d'un continent entier, le flambage provoque des séries de "creux" et de "bosses" secondaires.

Par exemple, la collision alpine, en Europe occidentale, est responsable de la formation d'autres reliefs secondaires dont l'importance diminue à mesure que l'on s'éloigne des Alpes : Massif central ("bosse")et Limagne ("creux"), la Sologne (creux), le Massif Armoricain et les Alpes Mancelles (Bosse, bien que liée aussi à l'ouverture de l'Atlantique), la Mer du Nord (creux, dont l'autre facteur explicatif est aussi l'ouverture de l'Atlantique), le Pays de Caux et le Pays de Bray (bosses), les marais et polders de la région de Calais et du Nord de la Picardie (creux), le Boulonnais, l'Artois les Ardennes et l'Eifel (Bosses), la Flandre (creux).

On pourrait décrire de la même façon le contrecoup himalayen : plateaux de Tibet (creux), Altaï (bosse), lac Baïkal (creux).