Flambage - Définition

Introduction

Flexion sous un effort de compression.

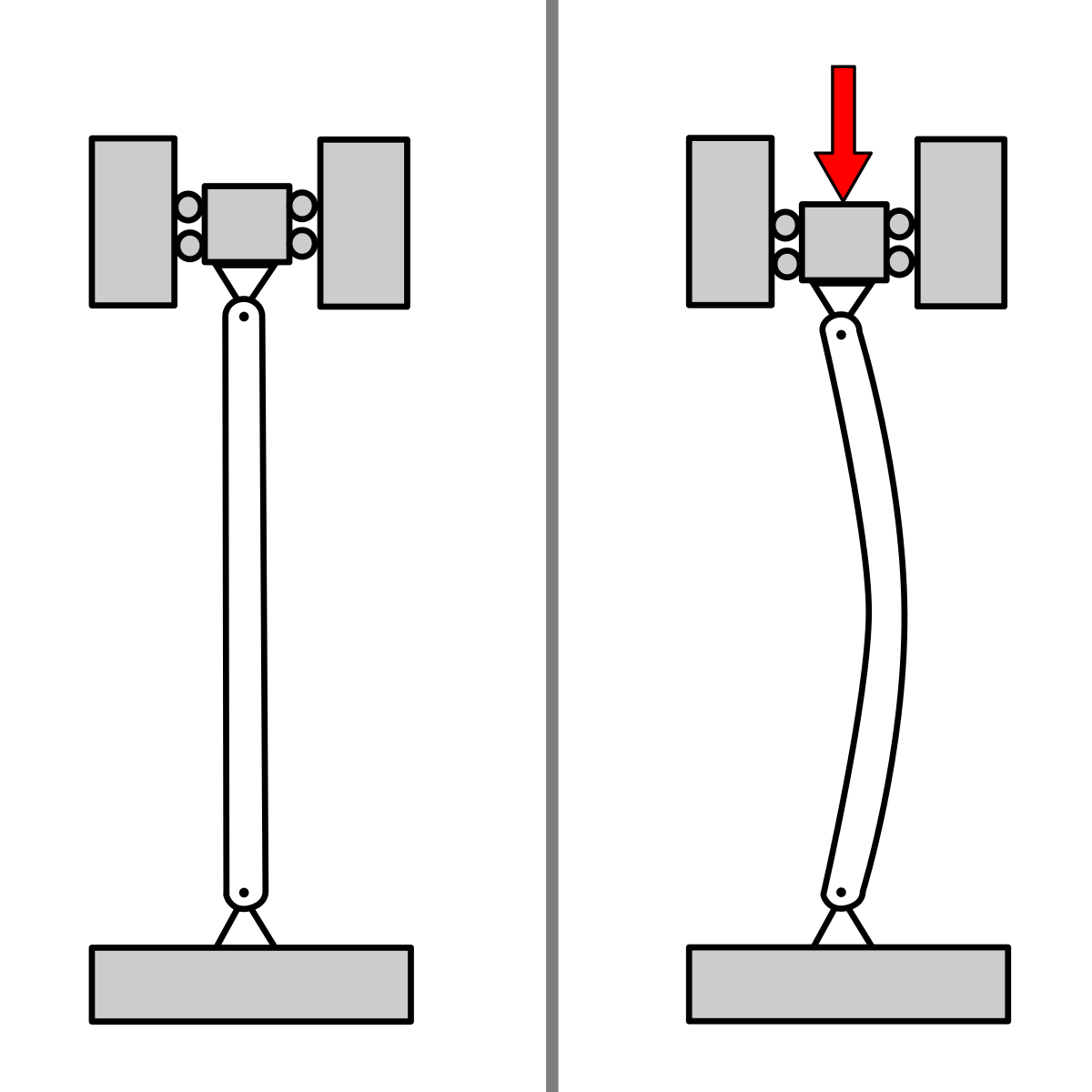
Le flambage ou flambement est un phénomène d'instabilité d'une structure, qui soumise à un effort normal de compression, a tendance à fléchir et se déformer dans une direction perpendiculaire à l'axe de compression (passage d'un état de compression à un état de flexion).

Le terme flambement est plutôt utilisé en mécanique de la structure.

Résistance des matériaux

Exemple d'une règle plate:

• Si les extrémités de la règle sont tenues et tirées, la rupture de la règle se produit quand les contraintes de traction deviennent supérieures à la résistance mécanique en traction du plastique.
• En revanche, si les extrémités de la règle sont tenues et comprimées dans le sens de la longueur, la règle va se plier et se briser avec un effort de compression bien plus faible que celui nécessaire à la rupture en traction.

Ce phénomène est appelé flambage.

En résistance des matériaux (RDM), le flambage est un phénomène d'instabilité élastique mis en évidence lorsqu'une poutre est comprimée, il se développe un moment de flexion parasite amplifié par les déformations et déplacements de la poutre chargée.

Ce phénomène n'est pas mis en évidence par le modèle RDM classique ou théorie des poutres car ce modèle considère que les efforts de calcul s'appliquent sur la structure non déformée (hypothèses de linéarisation externe et des petits déplacements de la mécanique des solides et de la RDM) et non sur la structure déjà en charge et déformée (théorie du second ordre).

Le flambage se produit d'autant plus facilement que la poutre est longue et de faible section. Le flambage dépend aussi du type de liaisons des extrémités de la poutre (les conditions d'appui).

Même si le terme poutre est employé ici, l'hypothèse RDM des petits déplacements doit être abandonnée pour que le modèle soit plus réaliste. Le modèle RDM doit être complété avec les hypothèses supplémentaires que les déformations restent petites mais que les déplacements peuvent être grands, cela permet de prendre en compte les phénomènes du second ordre négligés dans le modèle RDM.

Ce modèle RDM complété n'est plus linéaire, la résolution se fait par itérations successives jusqu'à convergence éventuelle du résultat. Ce modèle met en évidence des instabilités dont la charge critique d'Euler est un exemple simple.

La démonstration de la formule d'Euler est relativement complexe et sort du cadre de cet article. Comme cette formule ne fait intervenir que des termes issus du modèle RDM élastique linéaire (module de Young et géométrie de la poutre), on dit alors que le flambement est un phénomène d'instabilité élastique. En général le flambement élastique n'est que le début d'un comportement non linéaire bien plus complexe qui une fois amorcé conduit à des déformations plastiques dans le matériau puis à la ruine de la poutre.

Pour une poutre d'inertie constante soumise à un effort normal de compression simple, la charge critique de flambage théorique est donnée par la formule d'Euler:

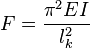
où

• E est le module de Young du matériau ;
• I est le moment quadratique de la poutre ;
• l_k est la longueur de flambement de la poutre.

Cette charge critique est évidemment limitée par la résistance en section de la poutre (à partir d'un certain élancement, la ruine est atteinte avant l'apparition du flambage). Dans le cas réel, la ruine par flambage est atteinte encore plus précocement en raison notamment des imperfections de production et de mise en œuvre (voir ci-dessous).

Une expérience de démonstration des modes de flambage d'Euler. Cette expérience montre comment les conditions aux limites (rotule, encastrée, libre) influent la charge critique d'une poutre fine (dans cette expérience, toutes les poutres sont identiques à leurs conditions aux limites près)

Le facteur l_k représente une longueur équivalente à celle d'une poutre rotulée-rotulée. Il s'agit de la distance séparant deux points d'inflexion de la déformée de la poutre. Ainsi,

• pour une poutre rotulée aux deux bouts, , la longueur de la poutre ;
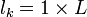
• pour une poutre encastrée - encastrée mobile (selon l'axe vertical),  ;
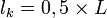
• pour une poutre encastrée-rotulée,  ;
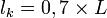
• pour une poutre encastrée-libre, .

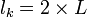
Attention : Le flambage est un phénomène d'instabilité élastique lié au module de Young et indépendant de la limite élastique, utiliser un acier de limite élastique supérieure pour diminuer le flambage est une erreur grave.