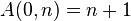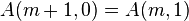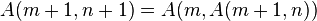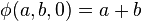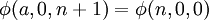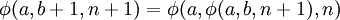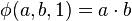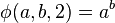Fonction d'Ackermann - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Dans la théorie de la récursivité, la fonction d'Ackermann (aussi appelée fonction d'Ackermann-Péter), est un exemple simple de fonction récursive non récursive primitive, trouvée en 1926 par Wilhelm Ackermann. Elle est souvent présentée sous la forme qu'en a proposé la mathématicienne Rózsa Péter, comme une fonction à deux paramètres entiers naturels comme arguments et qui retourne un entier naturel comme valeur, noté en général A(n, m).
Histoire
Dans les années 1920, Wilhelm Ackermann et Gabriel Sudan, alors étudiants sous la direction de David Hilbert, étudiaient les fondements de la calculabilité. Sudan est le premier à donner un exemple de fonction récursive mais non récursive primitive, appelée alors fonction de Sudan. Peu après et indépendamment, en 1928, Ackermann a publié son propre exemple de fonction récursive mais non récursive primitive. À l'origine, Ackermann considéra une fonction A (m, n, p) dépendant de trois variables, et consistant à calculer la puissance itérée p fois de m par n, c'est-à-dire m → n → p pour utiliser la notation de Conway.
Ackermann démontra que sa fonction A était bien une fonction récursive, i.e. une fonction qu'un ordinateur idéalisé peut calculer. Dans Sur l'infini, David Hilbert conjectura que la fonction d'Ackermann n'était pas primitivement récursive. Cette conjecture fut établie par Ackermann lui-même dans son article Zum Hilbertschen Aufbau der reellen Zahlen. Sur l'infini était l'article le plus important de Hilbert sur les bases des mathématiques, servant de cœur au programme de Hilbert pour fixer la base des nombres transfinis.
Une fonction semblable de seulement deux variables fut donnée plus tard par Rózsa Péter et Raphael Robinson, connue aujourd'hui sous le nom de fonction d'Ackermann.
Table de valeurs
| m\n | 0 | 1 | 2 | 3 | 4 | n |
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | n + 1 |
| 1 | 2 | 3 | 4 | 5 | 6 | n + 2 |
| 2 | 3 | 5 | 7 | 9 | 11 | 2n + 3 |
| 3 | 5 | 13 | 29 | 61 | 125 | 2n + 3 − 3 |
| 4 | 13 | 65533 | 265536 − 3 | A(3, 265536 − 3) | A(3, A(4, 3)) | 22...2 − 3 (n + 3 termes) |
| 5 | 65533 | A(4, 65533) | A(4, A(5, 1)) | A(4, A(5, 2)) | A(4, A(5, 3)) | |
| 6 | A(5, 1) | A(5, A(5, 1)) | A(5, A(6, 1)) | A(5, A(6, 2)) | A(5, A(6, 3)) |
Définition
La fonction d'Ackermann est définie récursivement comme suit :
Autrement dit :
Ackermann a lui-même initialement donné cette définition :
Elle satisfait aux égalités suivantes :
Description explicite
Intuitivement, la fonction d'Ackermann génère progressivement une multiplication par deux (additions réitérées), une exponentiation de base 2 (multiplications réitérées), une exponentiation réitérée, une réitération de cette opération, et ainsi de suite. Elle peut être exprimée en utilisant la notation des puissances itérées de Knuth :
- A(1, n) = 2 + (n + 3) - 3
- A(2, n) = 2 × (n + 3) - 3
- A(3, n) = 2 ↑ (n + 3) - 3
- A(4, n) = 2 ↑ (2 ↑ (2 ↑ (... ↑2))) - 3 (n + 3 deux)
- = 2↑↑(n + 3) - 3
- A(5, n) = 2↑↑↑(n + 3) - 3 etc.
On montre assez facilement par récurrence que:
- A(u, v) = 2↑(u-2)(v + 3) - 3