Formule de Brioschi - Définition

La terre est ronde, la preuve par les cartes marines

Des mathématiciens vivant sur une autre planète et n'ayant aucune possibilité d'observer la terre, ont obtenu un jeu de cartes marines couvrant une région du globe terrestre. Ce jeu leur suffit pour démontrer que cette région est une partie de sphère. Montrons comment.

Les cartes utilisent longitude et latitude et les échelles sont indiquées dans les 4 marges. Elles sont valables sur le bord correspondant de la carte.

Dans les marges gauche et droite les deux échelles sont les mêmes. Donc G_θ = 0. A l'aide d'une seconde carte couvrant la région au-dessus de la première, on observe que l'échelle des longitudes est encore la même que sur celle située au-dessous. Donc et G est constante.

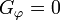
Par contre les échelles des marges haute et basse sont différentes. Le calcul de cette différence donne la valeur de . Sur les deux cartes ci-dessus on calcule la différence des différences et on obtient .

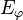
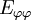
Les lignes θ=Cste et =Cste sont orthogonales, doncF=0.

Comme on vient de le voir, cela suffit à calculer la courbure aux points situés à la limite des deux cartes. En recommençant le calcul avec d'autres paires de cartes, les extra-terrestres trouvent toujours la même courbure, positive. D'après le théorème de Liebmann (1900) ils peuvent en déduire que la région couverte par le jeu de cartes est une partie de sphère.

Cas de la sphère

On utilise pour coordonnées locales la longitude et la latitude . Le rayon de la sphère est R.

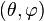
À la latitude , le parallèle a pour rayon . Donc un chemin suivant ce parallèle, depuis le point jusqu'au point a pour longueur . On a donc .

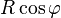
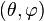
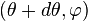
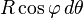
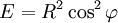
Un chemin suivant le méridien, depuis le point jusqu'au point a pour longueur . On a donc G = R².

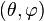
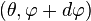
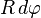
Puisque F = 0, on en déduit .

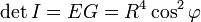
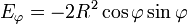
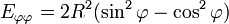
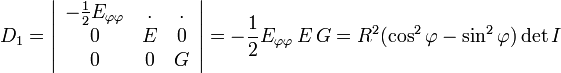
Il n'y a que deux dérivées à calculer, et et par conséquent

et

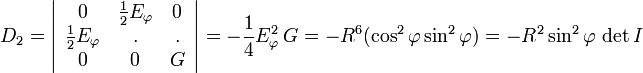
d'où et donc

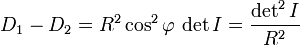
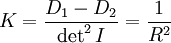
Sphère en fil de fer

Le raisonnement ci-dessus donne le mode de construction d'une sphère en fil de fer.