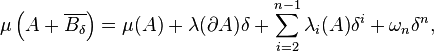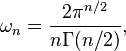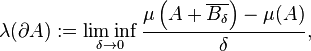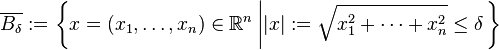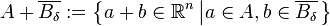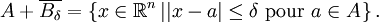Formule de Steiner-Minkowski - Définition
La liste des auteurs de cet article est disponible ici.
Remarques
Mesure de la surface
Pour un ensemble "suffisamment irrégulier" A, la quantité
Ensembles convexes
Quand l'ensemble A est convexe, la limite inférieure ci-dessus est une vraie limite et on peut montrer
où λi est une fonction continue sur A et ωn désigne la mesure (ou volume) de la boulé unité de
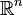
avec Γ désignant la fonction gamma.
Enoncé de la formule
Soit
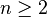
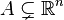
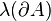
avec
désignant la boule fermée de rayon δ > 0, et
est la somme de Minkowski de A et
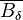
Exemple : volume et surface d'une boule
Prenons
-
-
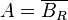
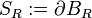
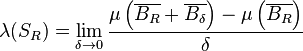
![= \lim_{\delta \to 0} \frac{[ (R + \delta)^{n} - R^{n} ] \omega_{n}}{\delta}](https://static.techno-science.net/illustration/Definitions/autres/a/a86bdb027e1d0657b3908b88845694f6_7f58cf5e4136bc73255011d23805247e.png)
- = nRn − 1ωn,
-
![= \lim_{\delta \to 0} \frac{[ (R + \delta)^{n} - R^{n} ] \omega_{n}}{\delta}](https://static.techno-science.net/illustrationWebp/Definitions/autres/a/a86bdb027e1d0657b3908b88845694f6_7f58cf5e4136bc73255011d23805247e.png)
avec ωn défini ci-dessus.
