Formule de Steiner-Minkowski - Définition

Introduction

En géométrie, les formules de Steiner-Minkowski sont des relations traitant d'un compact C d'un espace euclidien E. On ajoute en général une condition supplémentaire sur le compact, indiquant qu'il est soit convexe, soit de frontière homéomorphe à la sphère et paramétrable par une fonction de classe C² de la sphère dans l'espace euclidien.

La première formule indique que la frontière du compact est mesurable et que sa mesure est égale à la dérivée en 0 de la fonction de R⁺ dans lui même, qui à un scalaire ε associe le volume de C + ε.B. Ici, R⁺ désigne l'ensemble des nombres réels positif, B la boule unité et le signe + la somme de Minkowski. La mesure utilisée est celle de Lebesgue.

La deuxième formule indique que la mesure du volume de C + εB s'exprime comme un polynôme de degré la dimension de E, si ε est suffisamment petit.

La mesure de la frontière utilisée correspond au contenu n - 1 dimensionnel de Minkowski. Dans le cas où la frontière est paramétrable par une fonction de classe C², le contenu se confond avec la définition usuelle, c'est-à-dire celle obtenue avec la forme volume canonique. Dans le cas de la dimension 2, ce contenu, dans le cas où la frontière est convexe, se confond avec la longueur de l'arc qu'est la frontière, au sens de Jordan.

Les formules de Steiner-Minkowski sont utilisées conjointement avec le théorème de Brunn-Minkowski, pour prouver le Théorème isopérimétrique. Elles ont été ainsi nommées en l'honneur des mathématiciens lithuanien Hermann Minkowski et suisse Jakob Steiner.

Contenu de Minkowski

Une des difficultés de la première formule de Steiner-Minkowski, sous sa forme générale, est le sens à donner au mot mesure de la frontière. Comme le montre l'article longueur d'un arc, il existe différentes manières de définir cette mesure.

En dimension 2, si la frontière est le support d'un arc paramétré (I, f) injectif presque partout et de classe C¹, une première définition de la mesure m_f de cette frontière est la suivante :

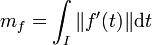
Cette définition se généralise bien, en dimension finie quelconque, si la frontière est l'ensemble d'arrivé d'un homéomorphisme φ de classe C¹ de la sphère S_n-1. La mesure de la frontière s'exprime comme l'intégrale sur la sphère de la valeur absolue déterminant jacobien de la fonction φ :

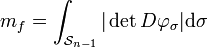
Dans le cas d'un convexe compact d'un espace dimension 2, la frontière est toujours le support d'un arc paramétrée injectif presque partout. En revanche, cet arc n'est pas nécessairement de classe C¹. Ceci n'est guère gênant, la définition de Jordan donne un sens à la longueur de l'arc, correspondant à une mesure 1 dimensionnel dans un espace de dimension 2. Dans le cas d'une dimension quelconque, la définition de Jordan ne se généralise pas (cf l'article Longueur d'un arc). Une autre définition prend le relai, celle du contenu n-1 dimensionnel de Minkowski.

• Le contenu p-dimensionnel de Minkowski d'un ensemble K d'un espace euclidien de dimension n, si p est un entier plus petit que n est la limite C_p,K, si elle existe, définie par :

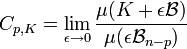
Ici, μ désigne la mesure de Lebesgue, B la boule unité et B_n-p la boule unité d'un espace de dimension n - p.

Cette définition est bien cohérente avec les deux précédentes :

• Soit C un convexe compact de E, un espace vectoriel de dimension n. Si la frontière F de C est l'ensemble d'arrivé d'un homéomorphisme φ de classe C¹ de la sphère S_n-1, le contenu n-1-dimensionnel de Minkowski C_n-1,F de F vérifie l'égalité :

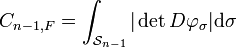
• Soit C un convexe compact de E, un espace vectoriel de dimension 2. Si la frontière F de C est le support de l'ensemble d'arrivé d'un lacet simple, le contenu 1-dimensionnel de Minkowski de C_1,F de F est égal à la longueur du lacet simple au sens de Jordan.

Un lacet ([a, b], f) est un arc paramétré sur un segment [a, b] tel que l'image de a soit égal à l'image de b par f. Le lacet est dit simple si la restriction de f à [a, b[ est injective.