Somme de Minkowski - Définition

Introduction

En géométrie, la somme de Minkowski est une opération sur les parties d'un espace euclidien. À deux parties A et B elle associe leur ensemble somme, formé des sommes d'éléments de A et de B :

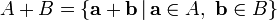
La somme de deux compacts est compact, il est ainsi possible de restreindre l'opération à cet ensemble, qui peut être munis d'une distance, dite de Hausdorff. La somme de Minkowski est alors une opération continue. De plus elle respecte les convexes, c'est-à-dire que la somme de deux convexes est encore convexe. La mesure de la somme de deux convexes vérifie une majoration, dite inégalité de Brunn-Minkowski.

La somme de Minkwoski intervient dans de nombreux domaines des mathématiques pures ou appliquées. Cet outils est à la base de nombreuses démonstrations de théorèmes isopérimétriques, visant à déterminer la partie de l'espace de plus vaste volume possible, la contrainte étant la donnée de la mesure de sa frontière. En géométrie euclidienne, on trouve les sphères de dimension n. La somme de Minkowski intervient aussi pour le comptage du nombre de face d'un polyèdre, résoudre des questions de pavages ou encore pour étudier la géométrie des convexes. Ils sont appliqués par exemple en cristallographie pour des raisons de pavages d'espace, en économie pour optimiser les productions possibles d'un groupe d'entreprises, ou encore pour étudier les mélanges.

Préambule

Exemples

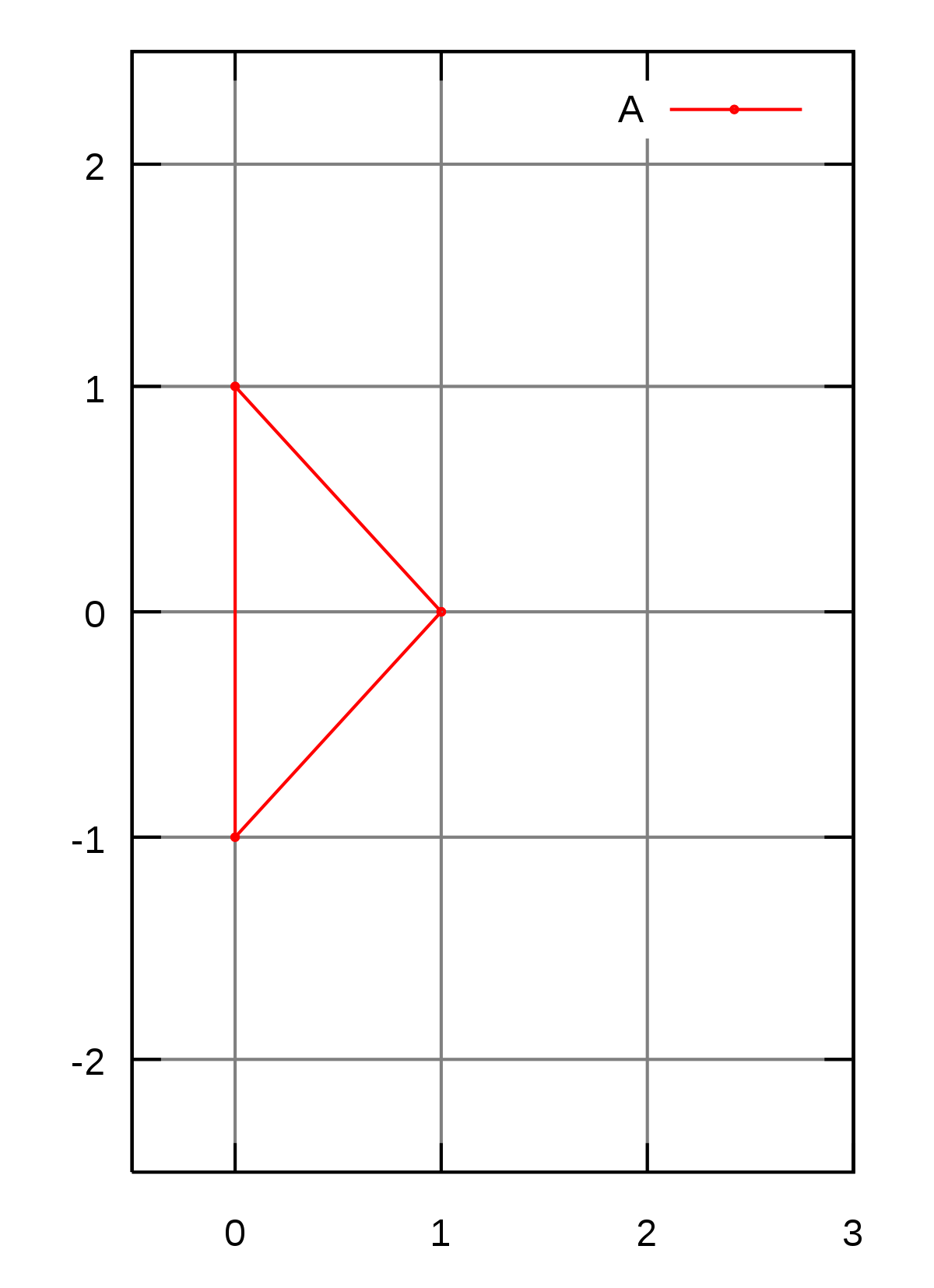
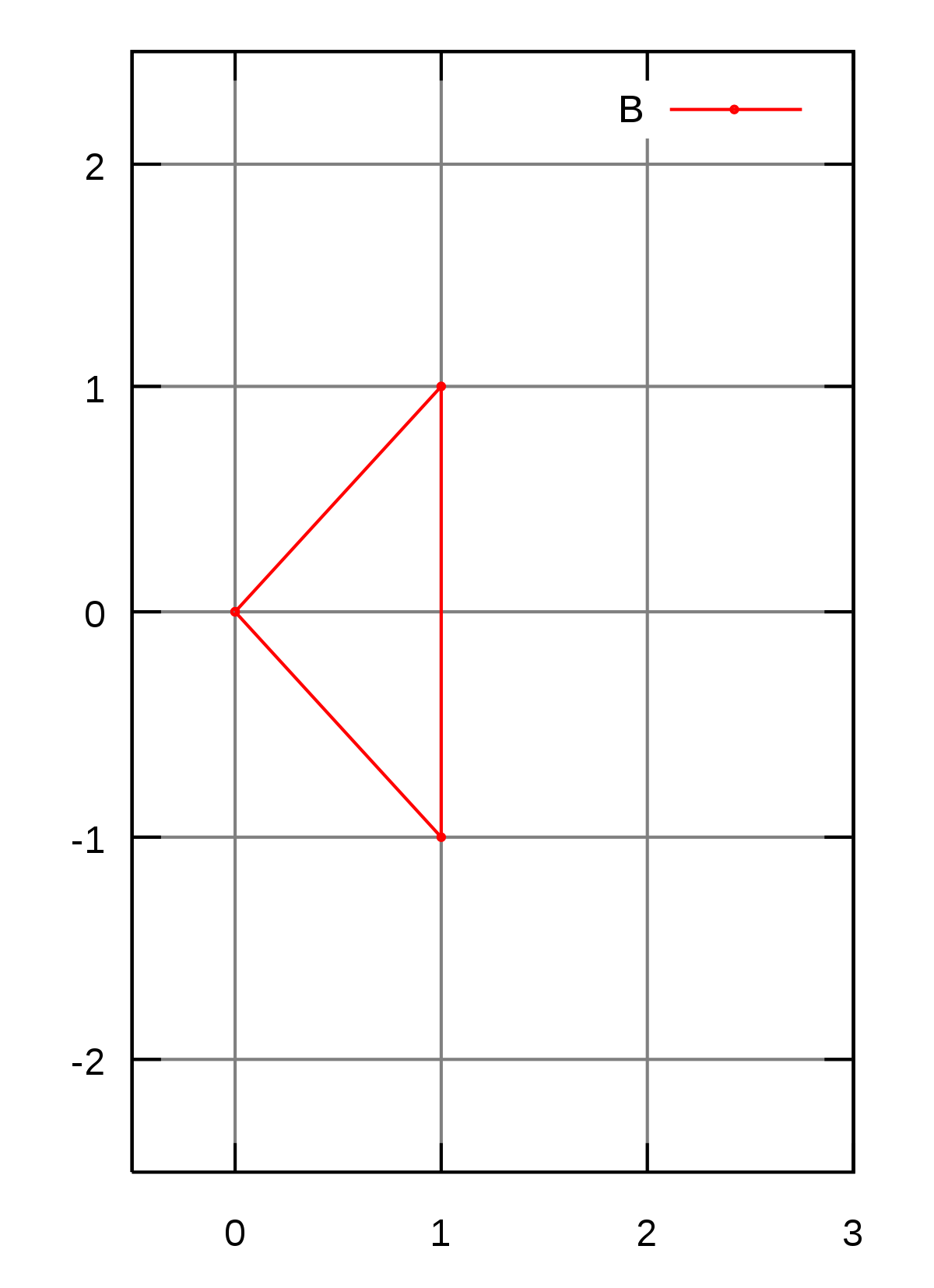
L'ensemble de A à gauche est un triangle dont les coordonnées des sommets sont (0,-1), (0,1) et (1,0). A droite est illustré un triangle semblable B, orienté différemment. Les coordonnées sont (0,0), (1,-1) et (1,1). Si les ensembles A et B sont deux triplets, on trouve :

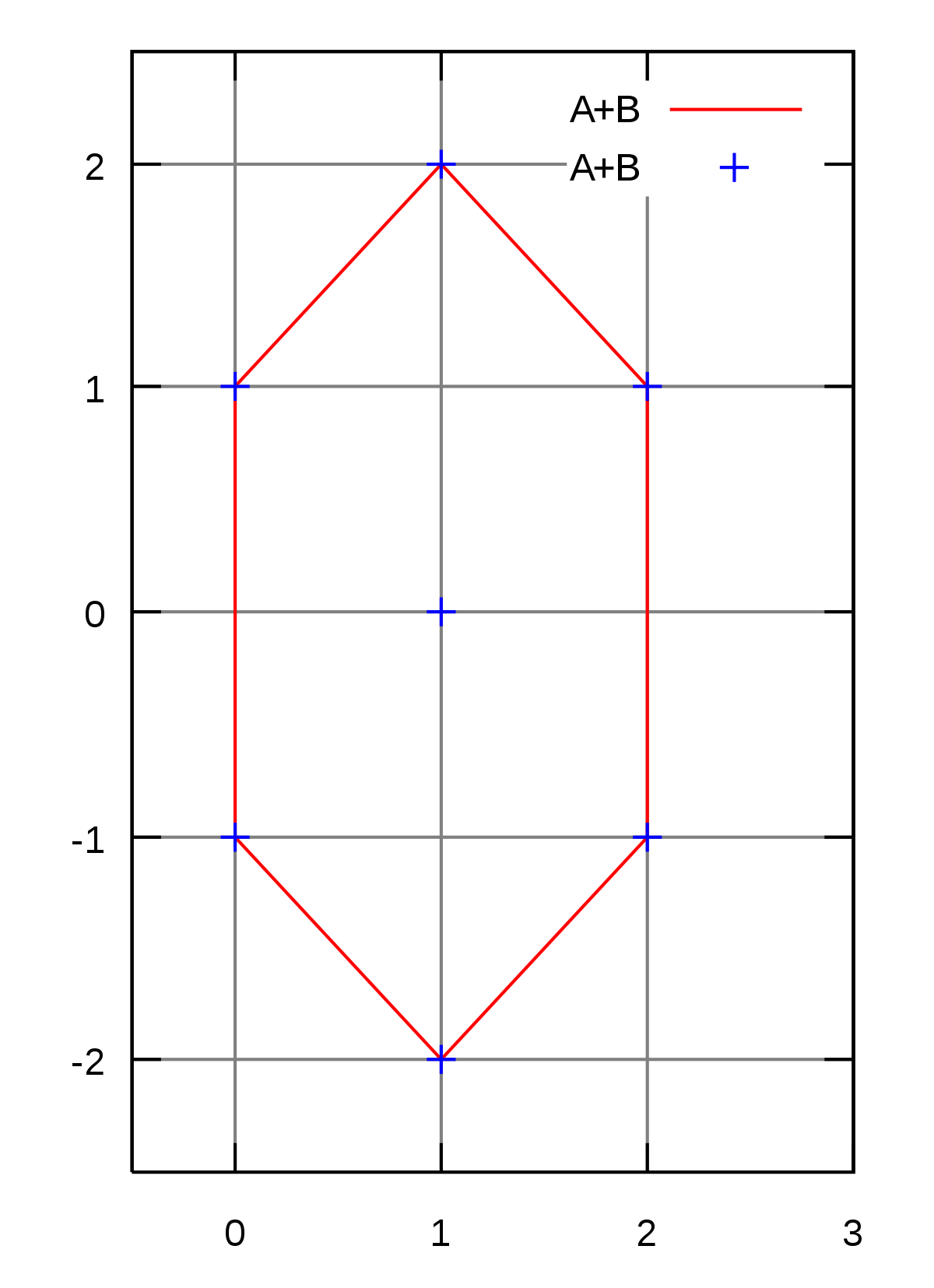
Si A et B sont les triangles illustrés en rouge, on trouve un hexagone, illustré par la figure en bas à droite.

De manière générale, la somme de deux polygones est encore un polygone. Cette propriété est vraie pour un polyèdre de dimension quelconque.

On peut remarquer l'analogie entre la somme de Minkowski et le produit de convolution. De manière imagée, on peut obtenir la surface de la somme A + B de deux ensembles en couvrant B de peinture et en faisant parcourir à son centre la surface A. Pour cette raison, cette somme de Minkowski est parfois appelée convolution de A et de B.

De manière évidente, la somme d'un ensemble A et d'un singleton {b} correspond à la translation de A par le vecteur b.

Il n'est guère plus complexe de se rendre compte que la somme de deux carrés est encore un carré. D'une manière plus générale, si C est un convexe, symétrique par rapport à l'origine, la somme C + C est égal au convexe 2C, ici 2C désigne l'homothétie de rapport 2. La démonstration est un peu plus subtile, elle est analogue au lemme préliminaire utilisé dans la démonstration du théorème de Minkowski. Pour s'en rendre compte, on peut remarquer que tout élément de 2C est élément de C + C, réciproquement soit u + v un élément de C + C, il s'écrit aussi comme le double de 1/2(u + v), or cet élément est dans C.

On peut citer un dernier exemple, que l'on trouve dans l'article théorème isopérimétrique. Soient C un compact convexe d'un plan euclidien et P un polygone convexe dont les sommets sont tous sur la frontière de C et dont la plus grande arête est d'une longueur majorée par ε. Alors la somme de P et du disque de centre le vecteur nul et de rayon ε contient le compact convexe C. Cette propriété est une étape pour établir qu'il n'existe aucune surface d'aire plus grande que le disque de même périmètre.

Premières propriétés

Cette opération est commutative, associative, possède pour élément neutre le singleton {0}. Elle est en outre distributive par rapport à la réunion

.

D'un point de vue topologique

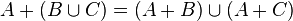
• la somme de deux parties ouvertes est ouverte (comme réunion de translatées de B par exemple)
• la somme de deux parties compactes est compacte (par la propriété de Bolzano-Weierstrass)
• la somme de deux partie convexe est convexe
• la somme, restreinte aux ensembles non vides fermés et bornés est une opération semi-continue supérieurement (cf Distance de Hausdorff).

Remarque : La somme de deux parties fermées n'est pas nécessairement fermée : par exemple en prenant dans le plan la droite des abscisses et l'hyperbole xy=1, leur somme forme le plan privé d'une droite.