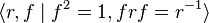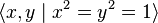Groupe diédral - Définition

Groupe diédral infini

En plus des groupes diédraux finis, on trouve le groupe diédral infini D_∞.

Tout groupe diédral est généré par une rotation r et une réflexion. Si la rotation est un multiple rationnel d’une rotation totale, alors il existe un entier n tel que rⁿ soit l’identité, et on est en présence d’un groupe diédral fini d’ordre 2n. Mais si la rotation n’est pas un multiple rationnel d’une rotation totale, alors il n’existe pas de tel n et le groupe résultant a un nombre infini d’éléments ; on le note D_∞. Il admet pour présentation

et est isomorphe au produit semi-direct de Z par C₂, ainsi qu’au produit libre C₂ * C₂. Il s’agit de l’automorphisme de groupes du graphe constitué d’un chemin infini vers les deux extrémités. De façon équivalente, il s’agit du groupe des isométries de Z.

Bibliographie

• Jean-Pierre Serre, Représentations linéaires des groupes finis
• Algèbre générale, Bernard Charles et denis Allouch, PUF, Paris 1984