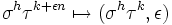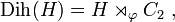Groupe diédral - Définition

Propriétés

Le sous-ensemble des rotations est un sous-groupe normal.

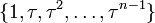
Certaines propriétés des groupes diédraux D_n avec n ≥ 3 dépendent de la parité de n. Elles peuvent souvent facilement être déduites de la représentation géométrique de ce groupe.

• Le centre de D_n est constitué seulement de l'identité si n est impair, mais si n est pair le centre a deux éléments : l'identité et l'élément τ^{n / 2}.
• Pour n impair, le groupe D_2n est isomorphe au produit direct de D_n et d'un groupe cyclique d'ordre 2. Cet isomorphisme est donné par :

où D_2n est l'ensemble de départ D_n*C₂ celui d'arrivée, h et ε étant définis modulo 2, et k modulo n. Les générateurs des groupes diédraux sont choisis comme dans la première partie de l'article.

• Toutes les réflexions sont conjuguées les unes les autres dans le cas où n est impair, mais elles sont contenues dans deux classes de conjugaison si n est pair.
• Si m divise n, alors D_n a n / m sous-groupes de type D_m, et un sous-groupe cyclique C_m. Par conséquent, le nombre total de sous-groupes de D_n (n ≥ 1), est égal à d (n) + σ (n), où d (n) est le nombre de diviseurs positifs de n et σ (n) est la somme des diviseurs positifs de n (voir liste des petits groupes pour les cas n ≤ 8)

Groupe diédral généralisé

Pour tout groupe abélien H, le groupe diédral généralisé de H, noté Dih(H), est le produit semi-direct de H par C₂, l'action de C₂ sur H étant l'inversion, i.e.

où φ(0) est l'application identité et φ(1) l'inversion des éléments.

On obtient ainsi, si H et C₂ sont tous deux notés additivement :

(h₁, 0) * (h₂, t₂) = (h₁ + h₂, t₂)

(h₁, 1) * (h₂, t₂) = (h₁ − h₂, 1 + t₂)

pour tous h₁, h₂ dans H et t₂ dans C₂.

(Si C₂ est noté multiplicativement, ces deux formules se résument en (h₁, t₁) * (h₂, t₂) = (h₁ + t₁h₂, t₁t₂) .)

Le sous-groupe de Dih(H) constitué des éléments de la forme (h, 0) est un sous-groupe normal d'indice 2, isomorphe à H. Quant aux éléments de la forme (h, 1), chacun est son propre inverse.

Les classes de conjugaison sont

• les ensembles {(h,0 ), (−h,0 )}
• les ensembles {(h + k + k, 1) | k dans H }

Ainsi, pour tout sous-groupe M de H, les éléments correspondants (m,0) forment aussi un sous-groupe normal de Dih(H) isomorphe à M, et l'on a :

Dih(H) / M = Dih ( H / M )

Exemples :

• D_n = Dih(C_n).
  • Si n est pair il y a deux ensembles de la forme {(h + k + k, 1) | k dans H }, et chacun d'eux engendre un sous-groupe normal isomorphe à D_n/2. Ce sont deux sous-groupes du groupe des isométries d'un n-gone régulier, isomorphes mais distincts : tous deux contiennent les mêmes rotations, mais dans l'un des deux sous-groupes, chaque réflexion fixe deux des sommets, tandis que dans l'autre, les réflexions ne fixent aucun sommet.
  • Si n est impair il n'y a qu'un ensemble de la forme {(h + k + k, 1) | k dans H }.
• D_∞ = Dih(Z) ; il y a deux ensembles de la forme {(h + k + k, 1) | k dans H }, et chacun d'eux engendre un sous-groupe isomorphe à D_∞. Ce sont deux sous-groupes du groupe des isométries de Z, isomorphes mais distincts : tous deux contiennent les mêmes translations (par les entiers pairs), mais dans l'un des deux sous-groupes, chaque réflexion a un point fixe entier (son centre), tandis que dans l'autre, les réflexions sont sans point fixe entier (leurs centres sont des demi-entiers).
• Dih(S¹) est isomorphe au groupe orthogonal O(2,R) des isométries du plan euclidien qui fixent l'origine ou de façon équivalente, au groupe des isométries du cercle. Les rotations forment le groupe SO(2,R), isomorphe au groupe additif R/Z, et également isomorphe au groupe multiplicatif S¹ égal au cercle unité (constitué des nombres complexes de module 1). Dans ce dernier cas, l'une des réflexions (qui, avec les rotations, engendre tout le groupe), est la conjugaison complexe. Les sous-groupes normaux propres ne contiennent que des rotations. Les sous-groupes normaux discrets sont, pour chaque entier n, un sous-groupe cyclique d'ordre n, et les quotients sont isomorphes au même groupe Dih(S¹).
• Dih(Rⁿ ) est le groupe des translations et symétries centrales de Rⁿ (qui, si n > 1 n'épuisent pas toutes les isométries).
• Dih(H) pour n'importe quel sous-groupe de Rⁿ, par exemple un groupe discret ; dans ce cas, s'il agit dans les n directions, c'est un réseau.
  • Les sous-groupes discrets de Dih(R² ) qui contiennent des translations dans une seule direction sont les groupes de frise de types ∞∞ et 22∞.
  • Ceux qui contiennent des translations dans deux directions sont les groupes de papier peint (en) de types p1 et p2.
  • Les sous-groupes discrets de Dih(R³ ) qui contiennent des translations dans trois directions sont les groupes d'espace de systèmes réticulaires tricliniques.

Dih(H) est abélien si et seulement si le produit semi-direct est direct, c'est-à-dire si et seulement si chaque élément de H est son propre inverse, i.e. H est un 2-groupe abélien élémentaire : Dih(C₂^k) = C₂^k+1.